Question

【题目】一列动车从甲地开往乙地， 一列普通列车从乙地开往甲地，两车均匀速行驶并同时出发，设普通列车行驶的时间为 (小时)，两车之间的距离为 (千米)，如图中的折线表示与之间的函数关系，下列说法:①动车的速度是千米/小时；②点B的实际意义是两车出发后小时相遇；③甲、乙两地相距千米；④普通列车从乙地到达甲地时间是小时，其中不正确的有( )

A.个B.个C.个D.个

Answer 1

【答案】B

【解析】

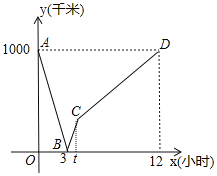
由x=0时y=1000可判断③；由运动过程和函数图像关系可判断②；求出普通列车速度，设动车的速度为x千米/小时，根据“动车3小时行驶的路程+普通列车3小时行驶的路程=1000”列方程求解可判断①；根据x=12时的实际意义可判断④.

解：③由x=0时，y=1000知，甲地和乙地相距1000千米，正确；

②如图，出发后3小时，两车之间的距离为0，可知点B的实际意义是两车出发后3小时相遇，正确；

①普通列车的速度是=千米/小时，

设动车的速度为x千米/小时，
根据题意，得：3x+3×=1000，
解得：x=250，
动车的速度为250千米/小时，错误；

④由图象知x=t时，动车到达乙地，
∴x=12时，普通列车到达甲地，
即普通列车到达终点共需12小时，错误；

故选B.