题目内容
已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A 、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2-4x-12=0的两个根.
、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2-4x-12=0的两个根.
(1)求出该二次函数的表达式及顶点坐标;
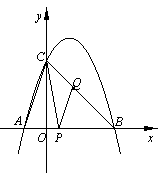
(2)如图,连接AC、BC,点P是线段OB上一个动点(点P不与点O、B重合),过点P作PQ∥AC交BC于点Q,当△CPQ的面积最大时,求点P的坐标.
 |
(1)由x2-4x-12=0,x=-2或 x=6…………………………………(1分)
x=6…………………………………(1分)
故A(-2,0)、B(6,0)、C(0,6). 二次函数y=a (x2-4x-12)中,-12a=6
∴a=-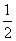 ,故二次函数y=-
,故二次函数y=-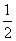 x2+2x+6,顶点坐标(2,8)………………… (3分)
x2+2x+6,顶点坐标(2,8)………………… (3分)
(2)设点P的横坐标为m,则0<m<6…………………………………………………(4分)
连结AQ,由PQ∥AC,知S△CPQ=S△APQ=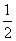 (m+2)·
(m+2)·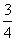 (6-m) ……………………(6分)
(6-m) ……………………(6分)
=- ( m2-4m-12)=-
( m2-4m-12)=- (m-2)2+6,当m=2时,S最大=6……………………(7分)
(m-2)2+6,当m=2时,S最大=6……………………(7分)
所以,当△CPQ的面积最大时,点P的坐标是(2,0)…………………………(8分)

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 =
= B.
B. C.1+2x=
C.1+2x=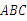 中,∠
中,∠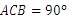 ,
,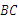 的垂直平分线
的垂直平分线 交
交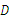 ,交
,交 于点
于点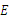 ,点
,点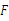 在
在 .
. 是平行四边形.
是平行四边形.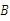 满足什么条件时,四边形
满足什么条件时,四边形


 ,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率. ,AE=6,则EC的长为
,AE=6,则EC的长为 . 6 B. 9
. 6 B. 9 
 的值为0,则x的值为 .
的值为0,则x的值为 . ,PB= .
,PB= . (2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.
(2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.
 。
。