题目内容
20.阅读理解:对于二次三项式x2+2ax+a2可以直接用公式法分解为(x+a)2的形式,但对于二次三项式x2+2ax-3a2,就不能直接用公式法了,我们可以在二次三项式x2+2ax-3a2中先加上一项a2,使其成为完全平方式,再减去a2这项,使整个式子的值不变.于是有x2+2ax-3a2=x2+2ax-3a2+a2-a=x2+2ax+a2-a2-3a2=(x+a)2-(2a)2=(x+3a)(x-a).像上面这样把二次三项式分解因式的方法叫做添(拆)项法.
(1)请用上述方法把x2-4x+3分解因式.
(2)多项式x2+2x+2有最小值吗?如果有,那么当它有最小值时,x是多少?
(3)请用上述方法把x4+x2+1分解因式.
分析 (1)用添项或拆项的方法分解因式;
(2)用添项或拆项的方法分解因式,再利用a2≥0,根据非负性来确定极值;
(2)用两次添项或拆项的方法分解因式,主要是要分解到不能再分解为止.
解答 解:(1)x2-4x+3=x2-4x+3+1-1=(x-2)2-1=(x-2+1)(x-2-1)=(x-1)(x-3);
(2)有最小值,
理由是:
x2+2x+2=x2+2x+1+1=(x+1)2+1,
∵(x+1)2≥0,
∴(x+1)2+1≥1,
∴当x=-1时,x2+2x+2有最小值,最小值是1,;
(3)x4+x2+1=x4+2x2-2x2+x2+1=(x4+2x2+1)-2x2+x2=(x2+1)2-x2=(x2+1+x)(x2+1-x)=(x2+x+1)(x2-x+1).
点评 此题是因式分解的应用,主要考查了添(拆)项的方法分解因式,添(拆)项是解本题的关键.

练习册系列答案
相关题目
8.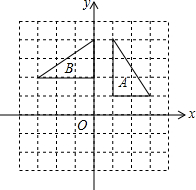 如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )
如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )
 如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )
如图,在边长为1的正方形网格中,图形B是由图形A旋转得到的,则旋转中心的坐标为( )| A. | (0,1) | B. | (-1,0) | C. | (0,0) | D. | (-2,-1) |
 如图,a∥b,∠1=50°,∠2=60°,则∠3=70°.
如图,a∥b,∠1=50°,∠2=60°,则∠3=70°.