Question

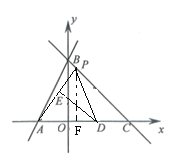
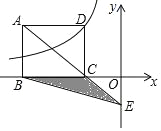
【题目】如图，直线分别与轴，轴交于点，，过点的直线交轴于点.为的中点，为射线上一动点，连结，，过作于点．

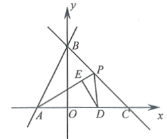
（1）直接写出点，的坐标：（______，______），（______，______）；

（2）当为中点时，求的长；

（3）当是以为腰的等腰三角形时，求点坐标；

（4）当点在线段（不与，重合）上运动时，作关于的对称点，若落在轴上，则的长为_______．

Answer 1

【答案】（1）-2，0；2，0；（2）；（3）当或时，是以为腰的等腰三角形；（4）．

【解析】

（1）先根据求出A,B的坐标，再把B点坐标代入求出b值，即可求解C点坐标，再根据为的中点求出D点坐标；

（2）先求出P点坐标得到，再根据即可求解；

（3）根据题意分① ②，即可列方程求解；

（4）根据题意作图，可得对称点即为A点，故AD=PD=4,设，作PF⊥AC于F点，得DF=2-x,PF=-x+4，利用Rt△PFD列方程解出x,得到P点坐标，再根据坐标间的距离公式即可求解．

（1）由直线AB的解析式为，

令y=0,得x=-2，

∴，

令x=0,得y=4，∴B（0，4）

把B（0，4）代入，求得b=4，

∴直线BC的解析式为

令y=0,得x=4，∴

∵为的中点

∴

故答案为：-2，0；2，0；

（2）由（1）得B（0，4），

当为的中点时，则，

∵为的中点，

∴轴，

，，

∴

∵，

∴

（3）∵点是射线上一动点，设，当是以为腰的等腰三角形时，

①若，，解得：，（舍去），此时；

②若，，解得：，此时.

综上，当或时，是以为腰的等腰三角形.

（4）∵关于的对称点，若落在轴上

∴点为A点，

∴AD=PD=4,

设，作PF⊥AC于F点，

∴DF=2-x,PF=-x+4，

在Rt△PFD中，DF2+PF2=DP2

即（2-x）2+（-x+4）2=42

解得x=3-（3+舍去）

∴P（3-，+1），

∴==

故答案为：．