题目内容
 如图,梯形ABCD中,AB∥CD,AB=a,CD=b(a<b),对角线AC与BD相交于O,△BOC的面积为梯形ABCD的面积的
如图,梯形ABCD中,AB∥CD,AB=a,CD=b(a<b),对角线AC与BD相交于O,△BOC的面积为梯形ABCD的面积的 ,则
,则 =________.
=________.

分析:由于AB∥OD,可得出△OAB∽△ODC;根据OA、OD的长,已知两个三角形的相似比;由相似三角形的面积比等于相似比的平方,即可求出
 .
.解答:由题意知:△AOB∽△DOC,则OA:OC=AB:CD=OB:OD=a:b,
∴
 =
=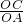 =
= ,
,∴
 =
=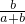 ,
,又
 =
= =
= ,
,∴
 =
= ,
,即
 =
=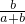 •
• =
= .
.∴2(a+b)2=9ab,
整理得:(2a-b)(a-2b)=0,
∵a<b,∴2a=b,
即
 =
= .
.点评:本题主要考查了相似三角形的性质:相似三角形的面积比等于相似比的平方.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2, 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.