Question

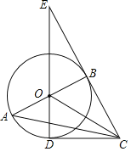
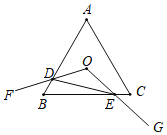
【题目】如图，等边△ABC的边长为4，点O是△ABC的外心，∠FOG＝120°．绕点O旋转∠FOG，分别交线段AB、BC于D、E两点．连接DE给出下列四个结论：①OD＝OE；②S△ODE＝S△BDE；③S四边形ODBE＝；④△BDE周长的最小值为6．上述结论中正确的个数是（ ）

A.1B.2C.3D.4

Answer 1

【答案】B

【解析】

连接OB，OC，易证△BOD≌△COE，因为OD=OE，将S四边形ODBE转化为S△BOC，故可得①③正确；利用特殊时刻：当D与B重合时，E与C重合，此时S△ODE＞0，而S△BDE=0，故②错误；因为△BOD≌△COE，所以BD=EC，所以当DE最小时，△BDE周长最小，利用勾股定理求出DE，找到DE的最小值即可解决问题．

如图，连接OB，OC，过点D作DM⊥BC于M．

（1）∵等边△ABC的边长为4，点O是△ABC的外心，∠FOG=120°，

∴易证∠BOD=∠COE，OB=OC，∠DBO=∠ECO=30°，

∴△BOD≌△COE，

∴OD=OE，故①正确；

（2）当D与B重合时，E与C重合，

此时S△ODE＞0，

而S△BDE=0，故②错误；

（3）∵△BOD≌△COE，

∴S四边形ODBE=S△ODB+S△BOE

=S△OCE+S△BOE

=S△BOC

=S△ABC

=，故③错误；

（4）∵△BOD≌△COE，

∴BD=EC，

∴△BDE周长=BD+BE+DE=BC+DE，

∵BC=4，

∴当DE最小时，△BDE周长最小．

设BD=x，则BM=x，DM=x，EC=BD=x，BE=4﹣x，

∴ME=BE﹣BM=4﹣x，

∴由勾股定理得：DE==，

∴DE的最小值为2，

∴△BDE周长的最小值为6，故④正确；

所以①④正确．

故选：B．