题目内容
如果一组数x1，x2，x3，x4，x5的平均数是
，则另一组数x1，x2+1，x3+2，x4+3，x5+4的平均数是
- A.
- B.+2
- C.+
- D.+10
B
分析：活学活用平均数计算公式：=
（x1+x2+x3+…xn）．将代入另一组数x1，x2+1，x3+2，x4+3，x5+4即可．
解答：根据题意=
（x1+x2+x3+x4+x5）；故（x1+x2+x3+x4+x5）=5，那么x1，x2+1，x3+2，x4+3，x5+4的平均数=（x1+x2+x3+x4+x5+1+2+3+4）=（x1+x2+x3+x4+x5）+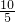
故该平均值应为+2．
故选B．
点评：本题考查平均数的求法=（x1+x2+x3+…xn）．学会运用整体代入的方法．
分析：活学活用平均数计算公式：
=（x1+x2+x3+…xn）．将代入另一组数x1，x2+1，x3+2，x4+3，x5+4即可．解答：根据题意
=（x1+x2+x3+x4+x5）；故（x1+x2+x3+x4+x5）=5，那么x1，x2+1，x3+2，x4+3，x5+4的平均数=（x1+x2+x3+x4+x5+1+2+3+4）=（x1+x2+x3+x4+x5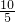）+故该平均值应为+2．故选B．
点评：本题考查平均数的求法
=（x1+x2+x3+…xn）．学会运用整体代入的方法． 
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
如果一组数x1，x2，x3，x4的平均数为
，则另一组数x1+2，x2+3，x3+4，x4+7的平均数是（ ）
| ? |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果一组数x1，x2，x3，x4，x5的平均数是
，则另一组数x1，x2+1，x3+2，x4+3，x5+4的平均数是（ ）
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
，则另一组数x1，x2+1，x3+2，x4+3，x5+4的平均数是（ ）
+2
+
+10
，则另一组数x1，x2+1，x3+2，x4+3，x5+4的平均数是（ ）
+2
+
+10