题目内容
已知:如图,直线AB经过⊙O上的点C,OA与⊙O 交于点D,若OA=OB,AD=CD,∠A=30°
(1)求证:直线AB是⊙O的切线;
(2)若AB=4 ,求OA的长.
,求OA的长.

(1)证明:连接OC.
∵AD=CD,∠A=30°,
∴∠A=∠ACD=30°,
∴∠ODC=∠A+∠ACD=60°,
∵OC=OD,
∴∠OCD=∠ODC=60°,
∴∠OCA=∠OCD+∠ACD=90°,
∴直线AB为⊙O的切线;
(2)解:∵OA=OB,OC⊥AB,AB=4 ,
,
∴BC=AC=2 ,
,
∵∠A=30°,
∴OA=2OC,
∵在Rt△ACO中,OA2=OC2+AC2,
∴AC=4.


练习册系列答案
相关题目
 cm C. 15πcm D. 15
cm C. 15πcm D. 15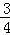 .
.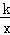 的图象经过点E,求k的值;
的图象经过点E,求k的值;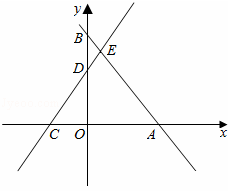

 点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到
点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到 线段BN.
线段BN.