题目内容
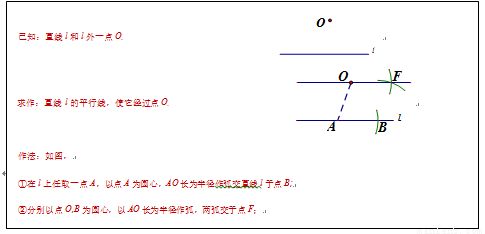
在正方形 ABCD 中,点 P 在射线 AB 上,连结 PC,PD,M,N 分别为 AB,PC 中点,连结 MN 交 PD 于点 Q.
(1)如图 1,当点 P 与点 B 重合时,求∠QMB 的度数;
(2)当点 P 在线段 AB 的延长线上时.
①依题意补全图2
②小聪通过观察、实验、提出猜想:在点P运动过程中,始终有QP=QM.小聪把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1延长BA到点 E,使AE=PB .要证QP=QM,只需证△PDA≌△ECB.
想法2:取PD 中点E ,连结NE,EA. 要证QP=QM只需证四边形NEAM 是平行四边形.
想 法3:过N 作 NE∥CB 交PB 于点 E ,要证QP=QM ,只要证明△NEM∽△DAP.
……
请你参考上面的想法,帮助小聪证明QP=QM. (一种方法即可)

练习册系列答案
相关题目


 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务. 时,已抢修道路 米;
时,已抢修道路 米; 是反比例函数,则
是反比例函数,则 的值为( )
的值为( ) D. 任意实数
D. 任意实数 ABC内接于
ABC内接于 O,AH
O,AH BC于点H,若AC=8,AH=6,
BC于点H,若AC=8,AH=6,  O的半径OC=5,则AB的值为( ).
O的半径OC=5,则AB的值为( ).
 C. 7 D.
C. 7 D. 
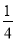 B.
B. 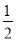 C.
C. 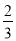 D.
D. 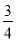

 .求 CD的长.
.求 CD的长.