Question

半径为r的三个圆⊙A、⊙B、⊙C两两外切，⊙O与这三个圆两两相切，则⊙O的半径为

(

2

3

3

-1)r或(

2

3

3

+1)r

．

Answer 1

分析：分内切与外切两种情况，根据相切两圆的性质及勾股定理进行解答即可．

解答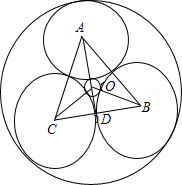：解：设待求圆半径为x，如图所示，
O为内切圆圆心，A、B、C分别为半径为r的圆的圆心，
由于三圆半径相等，图形具有轴对称性，延长AO交BC与D，D也为B、C圆的切点，
易知，∠ABO=∠OBD=60°÷2=30°，
在小三角形OBD中，又有∠ODB=90°，
∴OD=

OB2-BD2

=

OB

2

，
即

(x+r)2-r2

=

x+r

2

，
计算得到：x=（

2 3

3

-1）r，
当外切时，外切圆半径为x=（

2 3

3

+1）r，
故答案为：（

2 3

3

-1）r或（

2 3

3

+1）r．

点评：此题主要考查了相切两圆的性质以及解直角三角形的应用，正确的构造直角三角形是解决此类问题的关键．