题目内容
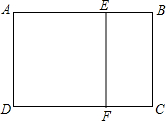 如果一个矩形的宽与长的比是黄金比,那么这个矩形称为黄金矩形.如图,已知四边形ABCD为黄金矩形,以它的宽为边在其内部作正方形AEFD,那么剩下的矩形BCFE也是一个黄金矩形,你能证明这个结论吗?
如果一个矩形的宽与长的比是黄金比,那么这个矩形称为黄金矩形.如图,已知四边形ABCD为黄金矩形,以它的宽为边在其内部作正方形AEFD,那么剩下的矩形BCFE也是一个黄金矩形,你能证明这个结论吗?考点:黄金分割,相似多边形的性质
专题:
分析:根据黄金分割设出矩形ABCD的长和宽,然后表示出矩形BCFE的宽,再求出宽与长的比值即可得证.
解答:证明:设矩形ABCD的长为x,
∵四边形ABCD为黄金矩形,
∴宽BC为
x,
∵四边形AEFD是正方形,
∴BE=x-
x=
x,
∴
=
=
=
=
=
,
∴BE与BC的比是黄金比,
∴剩下的矩形BCFE也是一个黄金矩形.
∵四边形ABCD为黄金矩形,
∴宽BC为
| ||
| 2 |
∵四边形AEFD是正方形,
∴BE=x-
| ||
| 2 |
3-
| ||
| 2 |
∴
| BE |
| BC |
| ||||
|
3-
| ||
|
(3-
| ||||
(
|
2
| ||
| 4 |
| ||
| 2 |
∴BE与BC的比是黄金比,
∴剩下的矩形BCFE也是一个黄金矩形.
点评:本题考查了黄金分割,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键,要熟记黄金分比.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
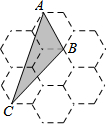 如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
 图中的四个小三角形都是等边三角形,边长为2cm,能通过平移△ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
图中的四个小三角形都是等边三角形,边长为2cm,能通过平移△ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.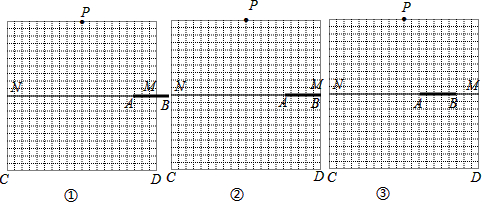
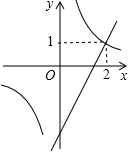 如图,已知反比例函数
如图,已知反比例函数