题目内容
 如图,AB为⊙O的弦,BD切⊙O于点B,OD⊥OA,OD与AB相交于点C.求证:BD=CD.
如图,AB为⊙O的弦,BD切⊙O于点B,OD⊥OA,OD与AB相交于点C.求证:BD=CD.考点:切线的性质
专题:证明题
分析:连结OB,根据切线的性质得OB⊥BD,则∠1+∠2=90°,由OD⊥OA得∠AOC=90°,则∠A+∠4=90°,利用∠1=∠A得到∠2=∠4,再根据对顶角相等得∠3=∠4,所以∠2=∠3,然后根据等腰三角形的判定得到DB=BC.
解答: 解:连结OB,如图,
解:连结OB,如图,
∵BD切⊙O于点B,
∴OB⊥BD,
∴∠1+∠2=90°,
∵OD⊥OA,
∴∠AOC=90°,
∴∠A+∠4=90°,
∵OA=OB,
∴∠1=∠A,
∴∠2=∠4,
而∠3=∠4,
∴∠2=∠3,
∴DB=BC.
 解:连结OB,如图,
解:连结OB,如图,∵BD切⊙O于点B,
∴OB⊥BD,
∴∠1+∠2=90°,
∵OD⊥OA,
∴∠AOC=90°,
∴∠A+∠4=90°,
∵OA=OB,
∴∠1=∠A,
∴∠2=∠4,
而∠3=∠4,
∴∠2=∠3,
∴DB=BC.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
已知△ABC∽△A′B′C′,且相似比为2.则( )
| A、∠A是∠A′的2倍 |
| B、∠A′是∠A的2倍 |
| C、AB是A′B′的2倍 |
| D、A′B′是AB的2倍 |
在反比例函数y=-
的图象上,坐标为整数的点的个数为( )
| 6 |
| x |
| A、4个 | B、6个 | C、8个 | D、10个 |
 如图,AM=AN,BM=BN,求证:△AMB≌△ANB.
如图,AM=AN,BM=BN,求证:△AMB≌△ANB.

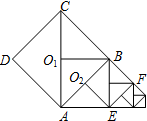 如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1,再以BE为对角线作第三个正方形EFBO2,如此作下去…则所作的第2013个正方形的面积是
如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1,再以BE为对角线作第三个正方形EFBO2,如此作下去…则所作的第2013个正方形的面积是 如图,据气象卫星显示,一股台风10h后将在距A城正东方向400km的B城登陆,并以每小时30km的速度向北偏西60°的BN方向移动,台风中心300km的范围会受到台风的影响.试问:A城是否会受到这次台风的影响?如果受影响,那么A城受台风影响的时间将有多长(结果保留整数)?如果不受影响,请说明理由.
如图,据气象卫星显示,一股台风10h后将在距A城正东方向400km的B城登陆,并以每小时30km的速度向北偏西60°的BN方向移动,台风中心300km的范围会受到台风的影响.试问:A城是否会受到这次台风的影响?如果受影响,那么A城受台风影响的时间将有多长(结果保留整数)?如果不受影响,请说明理由.