题目内容
如图，梯形ABCD的对角线交于O点，△ABO和△DCO的面积分别记为S1、S2，那么下列结论正确的是
- A.S1=S2
- B.S1＞S2
- C.S1＜S2
- D.只有当ABCD是等腰梯形时才有S1=S2
A
分析：根据同底等高判断△ABC和△DBC的面积相等，继而即可判断S1和S2的大小．
解答：观察图形可知，
∵△ABC和△DBC同底等高，
∴S△ABC=S△DBC，
∴S1+S△BOC=S△BOC+S2，
∴S1=S2，
故选A．
点评：本题主要考查梯形的知识以及三角形面积的等底等高或者等高等底情况的特性，难度适中．
分析：根据同底等高判断△ABC和△DBC的面积相等，继而即可判断S1和S2的大小．
解答：观察图形可知，
∵△ABC和△DBC同底等高，
∴S△ABC=S△DBC，
∴S1+S△BOC=S△BOC+S2，
∴S1=S2，
故选A．
点评：本题主要考查梯形的知识以及三角形面积的等底等高或者等高等底情况的特性，难度适中．
练习册系列答案
相关题目
如图，梯形ABCD的对角线交于点O，有以下四个结论：①△AOB∽△COD，②△AOD∽△ACB，③S△DOC：S△AOD=DC：AB，④S△AOD=S△BOC，其中始终正确的有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
14、如图，梯形ABCD的两条对角线交于点E，图中面积相等的三角形共有
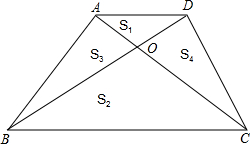如图，梯形ABCD的对角线AC、BD相交于点O，△ADO的面积记作S1，△BCO的面积记作S2，△ABO的面积记作S3，△CDO的面积记作S4，则下列关系正确是（ ）| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
16、如图，梯形ABCD的对角线交于点O，有以下三个结论：
如图，梯形ABCD的面积为34cm2，AE=BF，CE与DF相交于O，△OCD的面积为11cm2，则阴影部分的面积为