题目内容
8.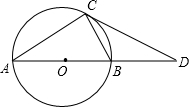 如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
分析 (1)连接OC,由AB是⊙O的直径可得出∠ACB=90°,即∠ACO+∠OCB=90°,由等腰三角形的性质结合∠BCD=∠A,即可得出∠OCD=90°,即CD是⊙O的切线;
(2)在Rt△OCD中,由勾股定理可求出OD的值,进而可得出BD的长.
解答 (1)证明:如图,连接OC.
∵AB是⊙O的直径,C是⊙O上一点,
∴∠ACB=90°,即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,
∴∠ACO=∠A=∠BCD,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴CD是⊙O的切线.
(2)解:在Rt△OCD中,∠OCD=90°,OC=3,CD=4,
∴OD=$\sqrt{O{C}^{2}+C{D}^{2}}$=5,
∴BD=OD-OB=5-3=2.
点评 本题考查了切线的判定与性质、勾股定理以及等腰三角形的性质,解题的关键是:(1)通过角的计算找出∠OCD=90°;(2)根据勾股定理求出OD的长度.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
13.一个三角形的三个内角的度数之比为1:2:3,则这个三角形一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰直角三角形 |
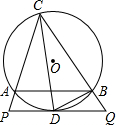 如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.
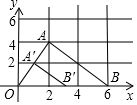 如图,△ABO三个顶点的坐标分别为A(2,4),B(6,0),O(0,0),以原点O为位似中心,把这个三角形缩小为原来的$\frac{1}{2}$,可以得到△A′B′O,已知点B′的坐标是(3,0),则点A′的坐标是(1,2).
如图,△ABO三个顶点的坐标分别为A(2,4),B(6,0),O(0,0),以原点O为位似中心,把这个三角形缩小为原来的$\frac{1}{2}$,可以得到△A′B′O,已知点B′的坐标是(3,0),则点A′的坐标是(1,2). 如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是8.
如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是8.