题目内容
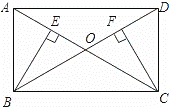
如图，矩形ABCD中，AC与BD交于点O，BE⊥AC，CF⊥BD，垂足分别为E，F．
求证：BE=CF．
BE=CF．解答： 证明：∵四边形ABCD为矩形，
∴AC=BD，则BO=CO．
∵BE⊥AC于E，CF⊥BD于F，
∴∠BEO=∠CFO=90°．
又∵∠BOE=∠COF，
∴△BOE≌△COF．
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
如图，矩形ABCD中，AC与BD交于点O，BE⊥AC，CF⊥BD，垂足分别为E，F．
求证：BE=CF．
BE=CF．解答： 证明：∵四边形ABCD为矩形，
∴AC=BD，则BO=CO．
∵BE⊥AC于E，CF⊥BD于F，
∴∠BEO=∠CFO=90°．
又∵∠BOE=∠COF，
∴△BOE≌△COF．
阅读快车系列答案
B. 3x2 C. 2xy3 D. 2x 3
，并将解集在数轴上表示出来．
线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是（ ）
（x＞0）的图象上，则△OAB的面积等于 ．
的相反数是（ ）
AD；
的解为x=_______．