题目内容
三枚硬币:第一枚的正面贴上红色标签,反面贴上蓝色;第二枚的正面贴上蓝色标签,反面贴上黄色;第三枚的正面贴上黄色标签,反面贴上红色.同时抛三枚,则三枚硬币落地后颜色各不相同的概率是多少?
∴一共有8种情况,三枚硬币落地后颜色各不相同的有2种情况,
∴三枚硬币落地后颜色各不相同的概率是
| 2 |
| 8 |
| 1 |
| 4 |

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案取四枚硬币,第一枚正、反面贴上1、2;第二枚正、反面贴上2、3;第三枚正、反贴上3、4;第四枚正、反面贴上4、1.同时抛四枚硬币,将硬币落地后的机会填在下面横线上.
|
(1)和为7 |
(2)和为10 |
(3)和为11 |
(4)和为13 |
|
(5)和为奇数 |
(6)和为9或12 |
(1) (2) (3) (4) (5) (6) .
掷两枚硬币,规定落地后,国徽朝上为正,国徽朝下为“反”,则会出现以下三种情况.

“正正” “反反”
“正反”
分别求出每种情况的概率.
(1)小刚做法:通过列表可知,每种情况都出现一次,因此各种情况发生的概率均占 .
.
| 可能出现的情况 | 正正 | 正反 | 反反 |
| 概率 |  |  |  |

小敏的做法:
| 第一枚硬币的可能情况 第二枚硬币的可能情况 | 正 | 反 |
| 正 | 正正 | 反正 |
| 反 | 正反 | 反反 |
 .“正反”的情况发生的概率为
.“正反”的情况发生的概率为 ,“反反”的情况发生的概率为
,“反反”的情况发生的概率为 .
.(1)以上三种做法,你同意哪种,说明你的理由;
(2)用列表法求概率时要注意哪些?
掷两枚硬币,规定落地后,国徽朝上为正,国徽朝下为“反”,则会出现以下三种情况.



分别求出每种情况的概率.
(1)小刚做法:通过列表可知,每种情况都出现一次,因此各种情况发生的概率均占 .
.
|
可能出现的情况 |
正正 |
正反 |
反反 |
|
概率 |
|
|
|

小敏的做法:
|
第一枚硬币的可能情况 第二枚硬币的可能情况 |
正 |
反 |
|
正 |
正正 |
反正 |
|
反 |
正反 |
反反 |
通过以上列表,小敏得出:“正正”的情况发生概率为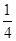 .“正反”的情况发生的概率为
.“正反”的情况发生的概率为 ,“反反”的情况发生的概率为
,“反反”的情况发生的概率为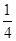 .
.
(1)以上三种做法,你同意哪种,说明你的理由;
(2)用列表法求概率时要注意哪些?
掷两枚硬币,规定落地后,国徽朝上为正,国徽朝下为“反”,则会出现以下三种情况.


“正正” “反反”

“正反”
分别求出每种情况的概率.
(1)小刚做法:通过列表可知,每种情况都出现一次,因此各种情况发生的概率均占 .
.
|
可能出现的情况 |
正正 |
正反 |
反反 |
|
概率 |
|
|
|

小敏的做法:
|
第一枚硬币的可能情况 第二枚硬币的可能情况 |
正 |
反 |
|
正 |
正正 |
反正 |
|
反 |
正反 |
反反 |
通过以上列表,小敏得出:“正正”的情况发生概率为 .“正反”的情况发生的概率为
.“正反”的情况发生的概率为 ,“反反”的情况发生的概率为
,“反反”的情况发生的概率为 .
.
(1)以上三种做法,你同意哪种,说明你的理由;
(2)用列表法求概率时要注意哪些?
