题目内容
如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC.(1)求证:AD是半圆O的切线;
(2)若BC=2,CE=
 ,求AD的长.
,求AD的长.
【答案】分析:(1)要证AD是半圆O的切线只要证明∠DAO=90°即可;
(2)由两组角对应相等的两个三角形相似可得到△DOA∽△ABC,据相似三角形的对应边成比例可得到AD的长.
解答:(1)证明:∵AB为半圆O的直径,
∴∠BCA=90°.
又∵BC∥OD,
∴OE⊥AC.
∴∠D+∠DAE=90°.
∵∠D=∠BAC,
∴∠BAC+∠DAE=90°.
∴AD是半圆O的切线.
(2)解:∵BC∥OD,
∴△AOE∽△ABC,
∵BA=2AO,
∴ =
= =
= ,又CE=
,又CE= ,
,
∴AC=2CE= .
.
在Rt△ABC中,
AB= =
= ,
,
∵∠D=∠BAC,∠ACB=∠DAO=90°,
∴△DOA∽△ABC.
∴ 即
即 .
.
∴ .
.
点评:此题考查学生对切线的判定及相似三角形的判定方法的掌握情况.
(2)由两组角对应相等的两个三角形相似可得到△DOA∽△ABC,据相似三角形的对应边成比例可得到AD的长.
解答:(1)证明:∵AB为半圆O的直径,
∴∠BCA=90°.
又∵BC∥OD,
∴OE⊥AC.
∴∠D+∠DAE=90°.
∵∠D=∠BAC,
∴∠BAC+∠DAE=90°.
∴AD是半圆O的切线.
(2)解:∵BC∥OD,
∴△AOE∽△ABC,
∵BA=2AO,

∴
 =
= =
= ,又CE=
,又CE= ,
,∴AC=2CE=
 .
.在Rt△ABC中,
AB=
 =
= ,
,∵∠D=∠BAC,∠ACB=∠DAO=90°,
∴△DOA∽△ABC.
∴
 即
即 .
.∴
 .
.点评:此题考查学生对切线的判定及相似三角形的判定方法的掌握情况.

练习册系列答案
相关题目
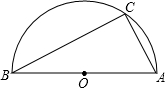
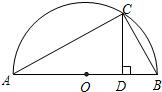 为D,AD=a,DB=b.
为D,AD=a,DB=b.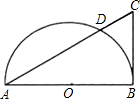 如图,AB为半圆O的直径,CB切半圆于点B,AC交半圆于点D,若CD=1,AD=3,则⊙O半径的长为
如图,AB为半圆O的直径,CB切半圆于点B,AC交半圆于点D,若CD=1,AD=3,则⊙O半径的长为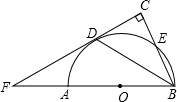 C,直线CD交BA的延长线于点F.
C,直线CD交BA的延长线于点F. 如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有
如图,AB为半圆O的直径,B1,B2,…,Bk是半圆上的k个点,满足BB1=B1B2=…Bk-1Bk,对于线段OB1,OB2,…,OBk,AB1,AB2,…,ABk,当k=4时,有