题目内容
如图，设△ABC是直角三角形，点D在斜边BC上，BD=4DC．已知圆过点C且与AC相交于F，与AB相切于AB的中点G．求证：AD⊥BF．
分析：作DE⊥AC于E，由切割线定理：AG2=AF•AC，可证明△BAF∽△AED，则∠ABF+∠DAB=90°，从而得出AD⊥BF．
解答：
证明：作DE⊥AC于E，
则AC=
AE，AB=5DE，
又∵G是AB的中点，
∴AG=
ED．
∴
ED2=AF•
AE，
∴5ED2=AF•AE，
∴AB•ED=AF•AE，
∴
=
，
∴△BAF∽△AED，
∴∠ABF=∠EAD，
而∠EAD+∠DAB=90°，
∴∠ABF+∠DAB=90°，
即AD⊥BF．
证明：作DE⊥AC于E，则AC=
| 5 |
| 4 |
又∵G是AB的中点，
∴AG=
| 5 |
| 2 |
∴
| 25 |
| 4 |
| 5 |
| 4 |
∴5ED2=AF•AE，
∴AB•ED=AF•AE，
∴
| AB |
| AE |
| AF |
| ED |
∴△BAF∽△AED，
∴∠ABF=∠EAD，
而∠EAD+∠DAB=90°，
∴∠ABF+∠DAB=90°，
即AD⊥BF．
点评：本题考查的是切割线定理，相似三角形的判定和性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=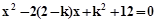
有实数根α、β.求实数k的取值范围；设
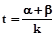，求t的最小值.
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
．容易知道一个角的大小与这个角的正对值也是相互唯一确定的．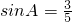
，其中A为锐角，试求sadA的值；