题目内容
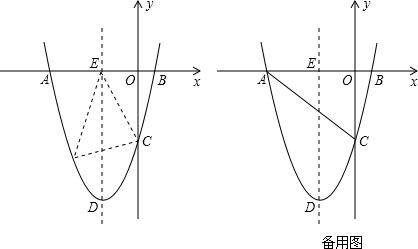
19. 已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)
已知二次函数h=x2-(2m-1)x+m2-m(m是常数,且m≠0)(1)证明:不论m取何值时,该二次函数图象总与x轴有两个交点;
(2)若A(n-3,n2+2)、B(-n+1,n2+2)是该二次函数图象上的两个不同点,求二次函数解析式和m的值;
(3)设二次函数h=x2-(2m-1)x+m2-m与x轴两个交点的横坐标分别为x1,x2(其中x1>x2),若y是关于m的函数,且y=2-$\frac{2{x}_{2}}{{x}_{1}}$,请结合函数的图象回答:当y<m时,求m的取值范围.
分析 (1)由抛物线与x轴有两个交点可知△>0,根据△=b2-4ac即可得到关于m的不等式,判断出△的取值范围即可;
(2)根据A(n-3,n2+2)、B(-n+1,n2+2)是该二次函数图象上的两个不同点,可以求出抛物线的对称轴,进而求出m的值和二次函数的解析式;
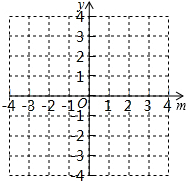
(3)首先令h=x2-(2m-1)x+m2-m=0,求出x1=m,x2=m-1,然后得到y与m的关系式,画出图象,结合图象进行作答.
解答 解:(1)由题意有△=[-(2m-1)]2-4(m2-m)=1>0.
即不论m取何值时,该二次函数图象总与x轴有两个交点;
(2)∵A(n-3,n2+2)、B(-n+1,n2+2)是该二次函数图象上的两个不同点,
∴抛物线的对称轴x=$\frac{n-3-n+1}{2}$=-1,
∴$\frac{2m-1}{2}$=-1,
∴m=-$\frac{1}{2}$,
∴抛物线解析式为h=x2+2x+$\frac{3}{4}$;
(3)令h=x2-(2m-1)x+m2-m=0,
解得x1=m,x2=m-1,
即y=2-$\frac{2{x}_{2}}{{x}_{1}}$=$\frac{2}{m}$,
作出图象如右:
当$\frac{2}{m}$=m时,
解得m=$±\sqrt{2}$,
当y<m时,m的取值范围为m>$\sqrt{2}$或-$\sqrt{2}$<m<0.
点评 本题考查的是抛物线与x轴的交点,根的判别式,解答此题的关键是利用数形结合的思想画出函数图象,再根据函数图象直接解答.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
9.在0,3,-1,$\frac{1}{2}$中最小的数是( )
| A. | 0 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
9.一元二次方程x2-9x+18=0的两根是一等腰三角形的底和腰,则这个等腰三角形的周长为( )
| A. | 12 | B. | 12或15 | C. | 15 | D. | 无法确定 |
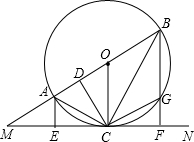 已知:如图,直线MN切⊙O于点C,AB为⊙O的直径,延长BA交直线MN于M点,AE⊥MN,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连结AC、BC,过点C作CD⊥AB,D为垂足,连结OC、CG.
已知:如图,直线MN切⊙O于点C,AB为⊙O的直径,延长BA交直线MN于M点,AE⊥MN,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连结AC、BC,过点C作CD⊥AB,D为垂足,连结OC、CG.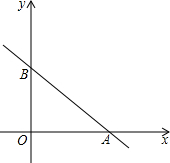 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.