题目内容
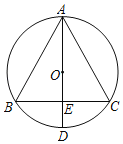
【题目】如图,△ABC内接于⊙O,AD为⊙O的直径,AD与BC相交于点E,且BE=CE.
(1)请判断AD与BC的位置关系,并说明理由;
(2)若BC=6,ED=2,求AE的长.
【答案】(1)AD⊥BC,理由见解析;(2)![]()
【解析】
(1)如图,连接OB、OC,根据全等三角形的性质即可得到结论;
(2)设半径OC=r,根据勾股定理即可得到结论.
(1)AD⊥BC,
理由:如图,连接OB、OC,

在△BOE与△COE中, 
∴△BOE≌△COE(SSS),
∴∠BEO=∠CEO=90°,
∴AD⊥BC;
(2)设半径OC=r,
∵BC=6,DE=2,
∴CE=3,OE=r﹣2,
∵CE2+OE2=OC2,
∴32+(r﹣2)2=r2,
解得r=![]() ,
,
∴AD=![]() ,
,
∵AE=AD﹣DE,
∴AE=![]() ﹣2=
﹣2=![]() .
.

练习册系列答案
相关题目