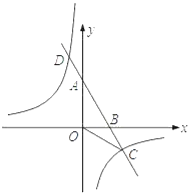
题目内容
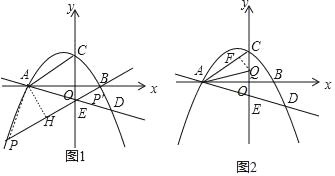
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣![]() x+c与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,直线y=﹣
x+c与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,直线y=﹣![]() x+b与抛物线相交于点A,D,与y轴交于点E,已知OB=
x+b与抛物线相交于点A,D,与y轴交于点E,已知OB=![]() ,OC=2.
,OC=2.
(1)求a,b,c的值;
(2)点P是抛物线上的一个动点,若直线PE∥AC,连接PA、PE,求tan∠APE的值;
(3)动点Q从点C出发,沿着y轴的负方向运动,是否存在某一位置,使得∠OAQ+∠OAD=30°?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ,b=-1,c=2;(2)
,b=-1,c=2;(2)![]() ;(3)点Q的坐标为(0,
;(3)点Q的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).
【解析】
(1)先确定B、C点坐标,再利用待定系数法求抛物线解析式得到a、c的值,然后解方程
﹣![]() x2﹣
x2﹣![]() x+2=0得A(﹣2
x+2=0得A(﹣2![]() ,0),然后把A点坐标代入y=﹣
,0),然后把A点坐标代入y=﹣![]() x+b得b的值;
x+b得b的值;
(2)易得直线AC的解析式为y=![]() x+2,E(0,1),利用直线平移得到直线PE的解析式为y=
x+2,E(0,1),利用直线平移得到直线PE的解析式为y=![]() x﹣1,则解方程组
x﹣1,则解方程组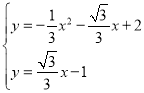 得P点坐标为(3
得P点坐标为(3![]() ,4)或
,4)或
(![]() ,0);当P点坐标为(
,0);当P点坐标为(![]() ,0),即P点与B点重合,易得tan∠APE=
,0),即P点与B点重合,易得tan∠APE=![]() ,此时∠ABH=30°;当P点坐标为(3
,此时∠ABH=30°;当P点坐标为(3![]() ,4)时,作AH⊥PE于H,根据面积法求出PH,然后根据正切定义计算tan∠APH的值;
,4)时,作AH⊥PE于H,根据面积法求出PH,然后根据正切定义计算tan∠APH的值;
(3)先计算出∠CAO=30°,∠ACO=60°,AC=2OC=4,则可判断∠CAQ=∠OAD,作QF⊥AC于F,如图,设Q(0,t),利用三角函数的定义得到CQ=2t,CF=![]() CF=
CF=![]() , FQ=
, FQ=![]() ,则AF=3+
,则AF=3+![]() t,通过Rt△AQF∽Rt△AEO得
t,通过Rt△AQF∽Rt△AEO得![]() (2﹣t):1=(3+
(2﹣t):1=(3+![]() t):
t):![]() ,解方程求出t得到此时Q点的坐标,易得Q(0,
,解方程求出t得到此时Q点的坐标,易得Q(0,![]() )关于x轴的对称点(0,
)关于x轴的对称点(0,![]() )也满足条件.
)也满足条件.
解:(1)∵OB=![]() ,OC=2,
,OC=2,
∴B(![]() ,0),C(0,2),
,0),C(0,2),
把B(![]() ,0),C(0,2)代入y=ax2﹣
,0),C(0,2)代入y=ax2﹣![]() x+c得
x+c得![]() ,解得
,解得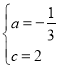 ,
,
∴抛物线解析式为y=﹣![]() x2﹣
x2﹣![]() x+2,
x+2,
当y=0时,﹣![]() x2﹣
x2﹣![]() x+2=0,解得x1=﹣2
x+2=0,解得x1=﹣2![]() ,x2=
,x2=![]() ,则A(﹣2
,则A(﹣2![]() ,0),
,0),
把A(﹣2![]() ,0)代入y=﹣
,0)代入y=﹣![]() x+b得﹣1+b=0,解得b=﹣1;
x+b得﹣1+b=0,解得b=﹣1;
(2)易得直线AC的解析式为y=![]() x+2,E(0,﹣1),
x+2,E(0,﹣1),
∵直线PE∥AC,
∴直线PE的解析式为y=![]() x﹣1,
x﹣1,
解方程组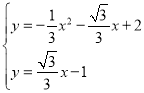 得
得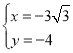 或
或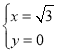 ,则P点坐标为(﹣3
,则P点坐标为(﹣3![]() ,﹣4)或(
,﹣4)或(![]() ,0);
,0);
当P点坐标为(![]() ,0),即P点与B点重合,tan∠APE=
,0),即P点与B点重合,tan∠APE=![]() =
=![]() ,此时∠ABH=30°,
,此时∠ABH=30°,
当P点坐标为(﹣3![]() ,﹣4)时,作AH⊥PE于H,如图2,
,﹣4)时,作AH⊥PE于H,如图2,
PB=![]() =8,
=8,
∵S△APB=![]() ,
,
∴AH=![]() ,
,
∴BH=![]() ,
,
∴PH=8﹣![]() ,
,
在Rt△APH中,tan∠APH=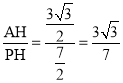 ,
,
综上所述,tan∠APE的值为![]() 或
或![]() ;
;
(3)存在.
如图2,在Rt△OAC中,tan∠OAC=![]() ,
,
∴∠CAO=30°,∠ACO=60°,
∴AC=2OC=4,
∵∠OAQ+∠OAD=30°,
∴∠CAQ=∠OAD,
作QF⊥AC于F,如图,设Q(0,t),
在Rt△CQF中,CQ=2﹣t,CF=![]() CF=
CF=![]() ,FQ=
,FQ=![]() ,
,
∴AF=AC﹣CF=4﹣![]() =3+
=3+![]() t,
t,
∵∠QAF=∠OAE,
∴Rt△AQF∽Rt△AEO,
∴FQ:OE=AF:AO,即![]() (2﹣t):1=(3+
(2﹣t):1=(3+![]() t):
t):![]() ,解得t=
,解得t=![]() ,此时Q(0,
,此时Q(0,![]() ),
),
易得Q(0,![]() )关于x轴的对称点(0,﹣
)关于x轴的对称点(0,﹣![]() )也满足条件,
)也满足条件,
综上所述,点Q的坐标为(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).