题目内容
【题目】如图，在3×3正方形方格中，有3个小正方形涂成了黑色，所形成的图案如图所示，图中每块小正方形除颜色外完全相同．
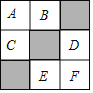
（1）一个小球在这个正方形方格上自由滚动，那么小球停在黑色小正方形的概率是多少？
（2）现将方格内空白的小正方形（A、B、C、D、E、F）中任取2个涂黑，得到新图案，请用列表或画树状图的方法求新图案是中心对称图形的概率．
【答案】（1）小球停在黑色小正方形的概率是
；（2）新图案是中心对称图形的概率是
．
【解析】
（1）根据题意和图形，可以求得小球停在黑色小正方形的概率；
（2）根据题意可以画出相应的表格，从而可以求得相应的概率．
解：（1）由题意可得，
小球停在黑色小正方形的概率是
，
即小球停在黑色小正方形的概率是；
（2）
共有30种等可能结果，中心对称的情况是：（BE）、（CD）、（AF），（EB），（DC），（FA），
则新图案是中心对称图形的概率是：
，
即新图案是中心对称图形的概率是．
练习册系列答案
相关题目
