题目内容
5.在同一直角坐标系中,若一次函数y=kx-2的图象与二次函数y=x2-1的图象没有公共点,则( )| A. | k>2 | B. | k<2且k≠0 | C. | -2<k<2且k≠0 | D. | k<-2或k>2 |
分析 一次函数y=kx-2的图象与二次函数y=x2-1的图象没有公共点,就是两函数解析式所组成的方程组无解,据此即可求得k的范围.
解答 解:根据题意得:$\left\{\begin{array}{l}{y=kx-2①}\\{y={x}^{2}-1②}\end{array}\right.$,
将①代入②得,kx-2=x2-1,
整理得,x2-kx+1=0,
由题意得△=(-k)2-4<0,
解得-2<k<2,
∵y=kx-2是一次函数,
∴k≠0,
∴-2<k<2且k≠0.
故选C.
点评 本题考查了二次函数与一次函数的性质,两函数图象没有交点,即由其组成的方程组无解.

练习册系列答案
相关题目
17.下列说法中,正确的有( )
①$\frac{3xy}{5}$的系数是$\frac{3}{5}$;②-22ab2的次数是5;③多项式mn2+2mn-3n-1的次数是3;④a-b和$\frac{xy}{2}$都是整式.
①$\frac{3xy}{5}$的系数是$\frac{3}{5}$;②-22ab2的次数是5;③多项式mn2+2mn-3n-1的次数是3;④a-b和$\frac{xy}{2}$都是整式.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.-$\frac{1}{2}$的倒数与3的和是( )
| A. | -$\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -5 | D. | 1 |
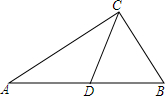 如图,已知△ABC中,∠C=90°,tanA=$\frac{1}{2}$,点D在边AB上,AD:DB=3:1,求cot∠DCB的值.
如图,已知△ABC中,∠C=90°,tanA=$\frac{1}{2}$,点D在边AB上,AD:DB=3:1,求cot∠DCB的值.