题目内容
 如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形),当四边形ABCD满足
如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形),当四边形ABCD满足考点:中点四边形
专题:
分析:根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
解答:解:当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下: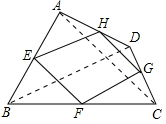
如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形FGH是平行四边形,
∴平行四边形EFGH是矩形;
故答案为:对角线互相垂直.

如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形FGH是平行四边形,
∴平行四边形EFGH是矩形;
故答案为:对角线互相垂直.
点评:本题主要考查了中点四边形的知识,牢记矩形的判定定理是解答本题的关键,难度中等.

练习册系列答案
相关题目
 如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)
如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母) 如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是
如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是
如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是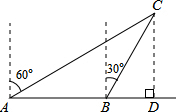 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于 如图,点P、Q分别是∠AOB的边OA、OB上的点.
如图,点P、Q分别是∠AOB的边OA、OB上的点.