题目内容
O是锐角三角形△ABC的外心,线段OA,BC的中点分别为M,N.∠ABC=4∠OMN,∠ACB=6∠OMN,则∠OMN=________.
12°
分析:连接ON.设∠OMN=x,根据已知条件和圆周角定理即可发现三角形OMN是等腰三角形,三角形的外心到三角形的三个顶点的距离相等,得到ON= OB,从而求得角的度数.
OB,从而求得角的度数.
解答: 解:连接ON.
解:连接ON.
设∠OMN=x,则∠ABC=4x,∠ACB=6x.
∴∠NOC=180°-10x,∠AOC=8x,
∴∠ONM=180°-(180°-10x+8x+x)=x,
∴△MON为等腰三角形,
又OA=OB,M是OA的中点,
∴ON= OB.
OB.
∴∠OBN=30°,
∴180°-10x=60°,
∴x=12°.
故答案为12°.
点评:此题综合运用了圆周角定理、三角形的外心的性质和直角三角形的性质.
分析:连接ON.设∠OMN=x,根据已知条件和圆周角定理即可发现三角形OMN是等腰三角形,三角形的外心到三角形的三个顶点的距离相等,得到ON=
 OB,从而求得角的度数.
OB,从而求得角的度数.解答:
 解:连接ON.
解:连接ON.设∠OMN=x,则∠ABC=4x,∠ACB=6x.
∴∠NOC=180°-10x,∠AOC=8x,
∴∠ONM=180°-(180°-10x+8x+x)=x,
∴△MON为等腰三角形,
又OA=OB,M是OA的中点,
∴ON=
 OB.
OB.∴∠OBN=30°,
∴180°-10x=60°,
∴x=12°.
故答案为12°.
点评:此题综合运用了圆周角定理、三角形的外心的性质和直角三角形的性质.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目


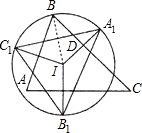 已知点I是锐角三角形ABC的内心,A1、B1、C1分别是点I关于边BC,CA,AB的对称点,若点B在△A1B1C1的外接圆上,则∠ABC等于
已知点I是锐角三角形ABC的内心,A1、B1、C1分别是点I关于边BC,CA,AB的对称点,若点B在△A1B1C1的外接圆上,则∠ABC等于