题目内容
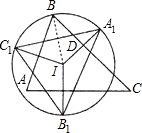 已知点I是锐角三角形ABC的内心,A1、B1、C1分别是点I关于边BC,CA,AB的对称点,若点B在△A1B1C1的外接圆上,则∠ABC等于
已知点I是锐角三角形ABC的内心,A1、B1、C1分别是点I关于边BC,CA,AB的对称点,若点B在△A1B1C1的外接圆上,则∠ABC等于分析:首先要抓住I是内心,即是三角形角平分线的交点,即可得∴∠DBI=
∠ABC,又由A1、B1、C1分别是点I关于边BC,CA,AB的对称点,可得ID=A1D=
IA1,∠BDI=90°,即可求得∠ABC的度数.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵I是锐角三角形ABC的内心,
∴∠DBI=
∠ABC,
∵A1、B1、C1分别是点I关于边BC,CA,AB的对称点,
∴ID=A1D=
IA1,∠BDI=90°,
∵点B在△A1B1C1的外接圆上,
∴IB=IA1,
∴ID=
IB,
∴∠IBD=30°,
∴∠ABC=60°.
故答案为:60°.
∴∠DBI=
| 1 |
| 2 |
∵A1、B1、C1分别是点I关于边BC,CA,AB的对称点,
∴ID=A1D=
| 1 |
| 2 |
∵点B在△A1B1C1的外接圆上,
∴IB=IA1,
∴ID=
| 1 |
| 2 |
∴∠IBD=30°,
∴∠ABC=60°.
故答案为:60°.
点评:此题考查了三角形的内心与对称性,以及直角三角形的知识.注意此题图形复杂,仔细识图,合理应用数形结合思想解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 OC,
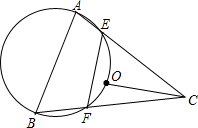
OC,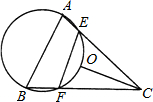 如图,已知点O是锐角三角形ABC的外心,过A、B、O三点的圆交于AC、BC于E、F,且EF=OC.
如图,已知点O是锐角三角形ABC的外心,过A、B、O三点的圆交于AC、BC于E、F,且EF=OC.