题目内容
将顶点坐标(-3,3)的抛物线向上平移1个单位,再向右平移2个单位,使其经过点(2,-5).
(1)求平移后抛物线的解析式;
(2)画出平移后的抛物线;
(3)求平移后的抛物线与x轴的交点坐标.
(1)求平移后抛物线的解析式;
(2)画出平移后的抛物线;
(3)求平移后的抛物线与x轴的交点坐标.
考点:二次函数图象与几何变换
专题:几何变换
分析:(1)先利用点的平移规律得到平移的抛物线的顶点坐标,则设顶点式y=a(x+1)2+4,然后把点(2,-5)代入求出a即可;
(2)利用描点法画出抛物线;
(3)利用求函数值为0时的自变量的值即可得到平移后的抛物线与x轴的交点坐标.
(2)利用描点法画出抛物线;
(3)利用求函数值为0时的自变量的值即可得到平移后的抛物线与x轴的交点坐标.
解答: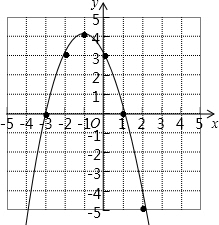 解:(1)∵点(-3,3)向上平移1个单位,再向右平移2个单位得到对应点的坐标为(-1,4),
解:(1)∵点(-3,3)向上平移1个单位,再向右平移2个单位得到对应点的坐标为(-1,4),
∴平移后的抛物线解析式可设为y=a(x+1)2+4,
∵点(2,-5)在抛物线y=a(x+1)2+4上,
∴a•9+4=-5,
解得a=-1.
∴平移后的抛物线解析式可设为y=-(x+1)2+4,
(2)如图,
(3)∵y=0时,-(x+1)2+4=0,
解得x1=-3,x2=1.
∴平移后的抛物线与x轴的交点坐标为(-3,0)和(1,0).
 解:(1)∵点(-3,3)向上平移1个单位,再向右平移2个单位得到对应点的坐标为(-1,4),
解:(1)∵点(-3,3)向上平移1个单位,再向右平移2个单位得到对应点的坐标为(-1,4),∴平移后的抛物线解析式可设为y=a(x+1)2+4,
∵点(2,-5)在抛物线y=a(x+1)2+4上,
∴a•9+4=-5,
解得a=-1.
∴平移后的抛物线解析式可设为y=-(x+1)2+4,
(2)如图,
(3)∵y=0时,-(x+1)2+4=0,
解得x1=-3,x2=1.
∴平移后的抛物线与x轴的交点坐标为(-3,0)和(1,0).
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
某超市出售的三种品牌的大米袋上(每种多于10袋),分别标有质量(25±0.1)kg,(25±0.2)kg,(25±0.15)kg的字样.从中任意拿出两袋,它们的质量最多相差( )
| A、0.4kg |
| B、0.35kg |
| C、0.3kg |
| D、0.25kg |
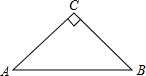 如图,△ABC是等腰Rt三角形,∠C=90°,AC=4.
如图,△ABC是等腰Rt三角形,∠C=90°,AC=4.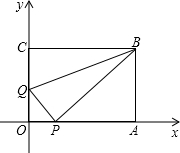 如图,在平面直角坐标系中,长方形OABC的两边分别在x轴和y轴上,且OA=14个单位长度,OC=8个单位长度,现有两个动点,P、Q,分别从O、C同时出发,P在线段OA上且以速度为1个单位长度/秒匀速运动,Q在线段CO上以0.5个单位长度/秒匀速运动,当其中一点到达线段的终点时,另一点也随之停止运动,设运动时间为t秒(t>0).
如图,在平面直角坐标系中,长方形OABC的两边分别在x轴和y轴上,且OA=14个单位长度,OC=8个单位长度,现有两个动点,P、Q,分别从O、C同时出发,P在线段OA上且以速度为1个单位长度/秒匀速运动,Q在线段CO上以0.5个单位长度/秒匀速运动,当其中一点到达线段的终点时,另一点也随之停止运动,设运动时间为t秒(t>0).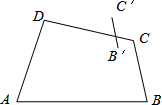 如图所示,已知四边形ABCD和线段B′C′,且线段BC与线段B′C′是位似图形.
如图所示,已知四边形ABCD和线段B′C′,且线段BC与线段B′C′是位似图形. 如图,厂房屋顶人字架△ABC(等腰三角形),上弦AB=AC,中柱AD(D为底边的中点)中柱AD与BC垂直吗?为什么?
如图,厂房屋顶人字架△ABC(等腰三角形),上弦AB=AC,中柱AD(D为底边的中点)中柱AD与BC垂直吗?为什么? (1)请画出图1这个轴对称图形的对称轴.
(1)请画出图1这个轴对称图形的对称轴.