题目内容
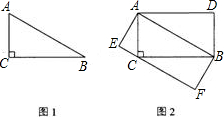
如图，△ABC是锐角三角形，以BC为直径作⊙O，AD是⊙O的切线，从AB上一点E作AB的垂线交AC的延长线于F，若| AB |
| AF |
| AE |
| AC |
求证：AD=AE．
分析：连接BN，根据BC为⊙O的直径，求证△ABN∽△AFE利用其对应边成比例得AE2=AN•AC，再利用切割线定理得出AD2=AN•AC，然后利用等量代换即可．
解答：
证明：如图，设AC交⊙O于点N．连接BN，
∵BC为⊙O的直径，
∴∠BNC=90°，
∴∠BNA=90°，
∵FE⊥AB，
∴∠AEF=90°=∠BNA，
∠BNA=∠FAE，
∴△ABN∽△AFE，
∴
=
，
∵
=
，
∴
=
，即AE2=AN•AC，
∵AD切⊙O于D，ANC为割线，
AD2=AN•AC，
即AD=AE．
证明：如图，设AC交⊙O于点N．连接BN，∵BC为⊙O的直径，
∴∠BNC=90°，
∴∠BNA=90°，
∵FE⊥AB，
∴∠AEF=90°=∠BNA，
∠BNA=∠FAE，
∴△ABN∽△AFE，
∴
| AB |
| AF |
| AN |
| AE |
∵
| AB |
| AF |
| AE |
| AC |
∴
| AN |
| AE |
| AE |
| AC |
∵AD切⊙O于D，ANC为割线，
AD2=AN•AC，
即AD=AE．
点评：此题主要考查学生对相似三角形的判定与性质和切割线定理的理解和掌握，证明此题的关键是作好辅助线：连接BN，求证出AE2=AN•AC，和AD2=AN•AC，这是此题的突破点．此题有一定难度，属于难题．
练习册系列答案
相关题目
如图，△ABC是锐角三角形，正方形DEFG的一边在BC上，其余两个定点在AB，AC上，记△ABC的面积为S1，正方形的面积为S2，则（ ）| A、S1≥2S2 | B、S1≤2S2 | C、S1＞2S2 | D、S1＜2S2 |
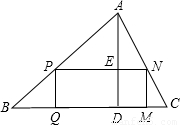
如图，△ABC是锐角三角形，BC=120，高AD=80，矩形PQMN的顶点P、N分别在AB、AC上，M、Q在BC上，AD与PN交于点E，请问矩形PQMN的面积什么时候最大，最大面积是多少？