题目内容
【题目】等腰![]() 被某一条直线分成两个等腰三角形,并且其中一个等腰三角形与原三角形相似,则等腰
被某一条直线分成两个等腰三角形,并且其中一个等腰三角形与原三角形相似,则等腰![]() 的顶角的度数是____.
的顶角的度数是____.
【答案】![]() 或
或![]() 或
或![]()
【解析】
因为题中没有指明是过顶角的顶点还是过底角的顶点,且其中一个等腰三角形与原三角形相似与故应该分三种情况进行分析,从而求解.
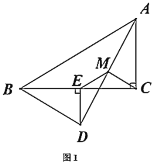
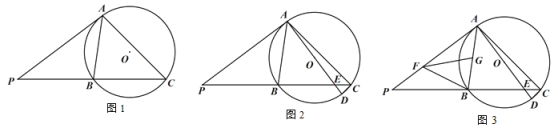
解:①如图1,∵AB=AC,当BD=CD,CD=AD,
∴∠B=∠C=∠BAD=∠CAD,
∵∠BAC+∠B+∠C=180°,
∴4∠B=180°,
∴∠B=45°,
∴∠BAC=90°.
此时易知∠BDA=∠BAC=90°,∠ABD=∠ABC= 45°,故![]() ∽
∽![]() ;
;
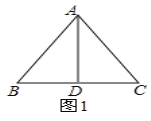
②如图2,∵AB=AC,AD=BD,AC=CD,
∴∠B=∠C=∠BAD,∠CAD=∠CDA,
∵∠CDA=∠B+∠BAD=2∠B,
∴∠BAC=3∠B,
∵∠BAC+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°,
∴∠BAC=108°.
此时易知∠BDA=∠BAC=108°,∠ABD=∠ABC= 36°, 故![]() ∽
∽![]() ;
;
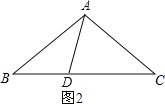
③如图3,∵AB=AC,AD=BD=BC,
∴∠B=∠C,∠BAC=∠ABD,∠BDC=∠C,
∵∠BDC=∠A+∠ABD=2∠BAC,
∴∠ABC=∠C=2∠BAC,
∵∠BAC+∠ABC+∠C=180°,
∴5∠BAC=180°,
∴∠BAC=36°.
此时易知∠CBA=∠CDB=72°,∠BAC=∠DBC=36°,故有![]() ∽
∽![]() ;
;
故答案为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目