题目内容
已知Rt△ABC,∠C=90°,AC=8cm,BC=6cm,若△PAB与△ABC全等,那么PC= .
考点:全等三角形的性质,勾股定理
专题:分类讨论
分析:利用勾股定理列式求出AB,然后分①点P与点C在AB的两侧时,AP与BC是对应边时,四边形ACBP是矩形,然后利用勾股定理列式计算即可得解;AP与AC是对应边时,根据对称性可知AB⊥PC,再利用三角形的面积列式计算即可得解;②点P与点C在AB的同侧时,利用勾股定理求出BD,再根据PC=AB-2BD计算即可得解.
解答: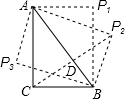 解:由勾股定理得,AB=
解:由勾股定理得,AB=
=
=10cm,
①点P与点C在AB的两侧时,若AP与BC是对应边,则四边形ACBP是矩形,
∴PC=AB=10cm,
若AP与AC是对应边,则△ABC和△ABP关于直线AB对称,
∴AB⊥PC
设AB与PC相交于点D,则S△ABC=
×10•CD=
×6×8,
解得CD=
,
∴PC=2CD=2×
=
,
②点P与点C在AB的同侧时,
由勾股定理得,BD=
=
=
,
∴PC=AB-2BD=10-2×
=
,
综上所述,PC的长为10或
或
.
故答案为:10或
或
.
 解:由勾股定理得,AB=
解:由勾股定理得,AB=| AC2+BC2 |
| 82+62 |
①点P与点C在AB的两侧时,若AP与BC是对应边,则四边形ACBP是矩形,
∴PC=AB=10cm,
若AP与AC是对应边,则△ABC和△ABP关于直线AB对称,
∴AB⊥PC
设AB与PC相交于点D,则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
解得CD=
| 24 |
| 5 |
∴PC=2CD=2×
| 24 |
| 5 |
| 48 |
| 5 |
②点P与点C在AB的同侧时,
由勾股定理得,BD=
| BC2-CD2 |
62-(
|
| 18 |
| 5 |
∴PC=AB-2BD=10-2×
| 18 |
| 5 |
| 14 |
| 5 |
综上所述,PC的长为10或
| 48 |
| 5 |
| 14 |
| 5 |
故答案为:10或
| 48 |
| 5 |
| 14 |
| 5 |
点评:本题考查了全等三角形的对应边相等的性质,勾股定理,轴对称性,难点在于分情况讨论,作出图形更形象直观.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
下列说法正确的是( )
| A、相等的角是对顶角 |
| B、在平面内,经过一点有且只有一条直线与已知直线平行 |
| C、两条直线被第三条直线所截,内错角相等 |
| D、在平面内,经过一点有且只有一条直线与已知直线垂直 |