Question

如图所示，在Rt△ABC中，∠A=60°，点E、F分别在AB、AC上，沿EF对折，使A落在BC上的D处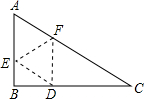，且FD⊥BC．
（1）确定点E在AB上和点F在AC上的位置；
（2）求证：四边形AEDF为菱形．

Answer 1

分析：（1）确定点E在AB上和点F在AC上的位置，就是求BE的长．
（2）易证四边形AEDF为平行四边形，只要再证明AE=ED即可．

解答：（1）解：∵△ABC为Rt△，∠A=60°，
∴∠C=30°．（1分）
∴AF=DF=

1

2

FC，即AF=

1

3

AC．（2分）
∵FD⊥BC，
∴∠BDE与∠EDF互余．
而∠EDF=∠A=60°，
∴∠BDE=30°．（3分）
∴BE=

1

2

ED=

1

2

AE，即BE=

1

3

AB．（4分）

（2）证明：∵∠BDE=30°，∠B=90°，
∴∠BED=60°=∠A，
∴ED∥AF．（5分）
∵AB⊥BC，FD⊥BC，
∴FD∥AE．（6分）
∴四边形AEDF为平行四边形．（7分）
又∵AE=ED，
∴四边形AEDF为菱形．（8分）

点评：本题主要考查了菱形的定义，有一组邻边相等的平行四边形是菱形．