题目内容
 如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别为1和2,则正方形的边长是
如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别为1和2,则正方形的边长是
- A.2
- B.

- C.3
- D.

B
分析:要求正方形的边长求AE,EB即可,其中AE已知,要求BE求证△ABE≌△BCF即可,即BE=CF,根据AE,CF可以求得AB的值.
解答:∵∠CBF+∠FCB=90°,
∠CBF+∠ABE=90°,
∴∠ABE=∠FCB,同理∠BAE=∠FBC,
∵AB=BC,
∴△ABE≌△BCF(ASA)
∴BE=CF,
在直角△ABE中,AE=1,BE=2,
∴AB= .
.
故选B.
点评:本题考查了正方形各边相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△ABE≌△BCF是解题的关键.
分析:要求正方形的边长求AE,EB即可,其中AE已知,要求BE求证△ABE≌△BCF即可,即BE=CF,根据AE,CF可以求得AB的值.
解答:∵∠CBF+∠FCB=90°,
∠CBF+∠ABE=90°,
∴∠ABE=∠FCB,同理∠BAE=∠FBC,
∵AB=BC,
∴△ABE≌△BCF(ASA)
∴BE=CF,
在直角△ABE中,AE=1,BE=2,
∴AB=
 .
.故选B.
点评:本题考查了正方形各边相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△ABE≌△BCF是解题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
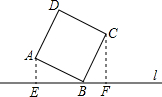 如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别为1和2,则正方形的边长是( )
如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别为1和2,则正方形的边长是( )| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
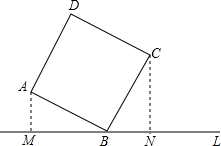 如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是
如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是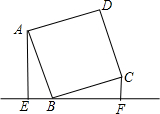 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是a和b,则正方形的边长是
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是a和b,则正方形的边长是 15、如图,直线l过正方形ABCD的顶点D,过A、C分别作直线l的垂线,垂足分别为E、F.若AE=4a,CF=a,则正方形ABCD的面积为
15、如图,直线l过正方形ABCD的顶点D,过A、C分别作直线l的垂线,垂足分别为E、F.若AE=4a,CF=a,则正方形ABCD的面积为 如图,直线d过正方形ABCD的顶点B,点A,C到直线d的距离分别是
如图,直线d过正方形ABCD的顶点B,点A,C到直线d的距离分别是