题目内容
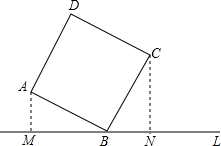如图，直线L过正方形ABCD的顶点B，点A、C到直线L的距离分别是1和2，则正方形的边长是分析：两直角三角形的斜边是正方形的两边，相等；有一直角对应相等；再根据正方形的角为直角，可得到有一锐角对应相等，易得两直角三角形全等，由三角形全等的性质可把2，1，正方形的边长组合到直角三角形内得正方形边长为
=
．
| 22+12 |
| 5 |
解答：
解：如图，
∵四边形ABCD是正方形，
∴AB=CD，∠ABM+∠CBN=90°，
而AM⊥MN，CN⊥BN，
∴∠BAM=∠CBN，∠AMB=∠CNB=90°，
∴△AMB≌△BCN（AAS），
∴BM=CN，
∴AB为
=
．
故答案为：
．
解：如图，∵四边形ABCD是正方形，
∴AB=CD，∠ABM+∠CBN=90°，
而AM⊥MN，CN⊥BN，
∴∠BAM=∠CBN，∠AMB=∠CNB=90°，
∴△AMB≌△BCN（AAS），
∴BM=CN，
∴AB为
| 22+12 |
| 5 |
故答案为：
| 5 |
点评：本题考查了正方形各边相等的性质，考查了直角三角形中勾股定理的运用，本题中求证△AMB≌△BCN是解题的关键．
练习册系列答案
相关题目
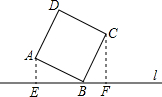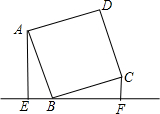如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是a和b，则正方形的边长是
15、如图，直线l过正方形ABCD的顶点D，过A、C分别作直线l的垂线，垂足分别为E、F．若AE=4a，CF=a，则正方形ABCD的面积为
如图，直线l过正方形ABCD的顶点B，点A，C到直线l的距离分别为1和2，则正方形的边长是（ ）| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
如图，直线d过正方形ABCD的顶点B，点A，C到直线d的距离分别是