题目内容
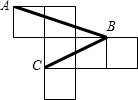
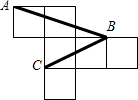如图为一个棱长为1的正方体的展开图，A、B、C是展开后小正方形的顶点，则∠ABC的度数为（ ）| A、30° | B、45° | C、50° | D、60° |
分析：连接AC，则AC，BC，AB的长度可以计算出来，根据AC，BC，AB判定△ABC为直角三角形，根据AC=BC判定∠ABC=45°．
解答：
解：连接AC，
则AC=
=
BC=
=
，
AB=
=
，
∵AC2+BC2=AB2
∴△ABC直角三角形，
∵AC=BC，
∴∠A=∠B=
=45°．
故选B．
解：连接AC，则AC=
| 22+1 |
| 5 |
BC=
| 22+1 |
| 5 |
AB=
| 32+1 |
| 10 |
∵AC2+BC2=AB2
∴△ABC直角三角形，
∵AC=BC，
∴∠A=∠B=
| 90° |
| 2 |
故选B．
点评：本题考查了直角三角形中勾股定理的运用，考查了等腰直角三角形底角为45°的性质，本题中求证△ABC是直角三角形是解题的关键．
练习册系列答案
相关题目
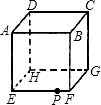如图是一个棱长为60cm的立方体ABCD-EFGH，一只小虫在棱EF上且距F点10cm的P处，它要爬到C点，则需要爬行的最短距离是（ ）| A、130 | ||
B、10
| ||
C、10
| ||
| D、不确定 |
如图为一个棱长为10cm的木制立方体和一个直径为12cm的球，能否在立方体上挖一个洞，使球通过？若能，请简单说明或画图示意；若不能，请说明理由．
