Question

【题目】已知等边△ABC的边长为2，

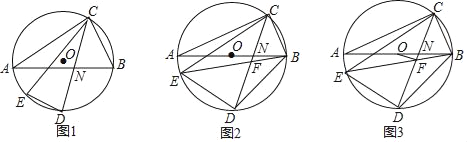
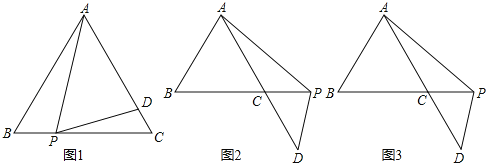
（1）如图1，在边BC上有一个动点P，在边AC上有一个动点D，满足∠APD＝60°，求证：△ABP～△PCD

（2）如图2，若点P在射线BC上运动，点D在直线AC上，满足∠APD＝120°，当PC＝1时，求AD的长

（3）在（2）的条件下，将点D绕点C逆时针旋转120°到点D'，如图3，求△D′AP的面积．

Answer 1

【答案】（1）见解析；（2）；（3）

【解析】

（1）先利用三角形的内角和得出∠BAP+∠APB＝120°，再用平角得出∠APB+∠CPD＝120°，进而得出∠BAP＝∠CPD，即可得出结论；

（2）先构造出含30°角的直角三角形，求出PE，再用勾股定理求出PE，进而求出AP，再判断出△ACP∽∠APD，得出比例式即可得出结论；

（3）先求出CD，进而得出CD'，再构造出直角三角形求出D'H，进而得出D'G，再求出AM，最后用面积差即可得出结论．

解：（1）∵△ABC是等边三角形，

∴∠B＝∠C＝60°，

在△ABP中，∠B+∠APB+∠BAP＝180°，

∴∠BAP+∠APB＝120°，

∵∠APB+∠CPD＝180°﹣∠APD＝120°，

∴∠BAP＝∠CPD，

∴△ABP∽△PCD；

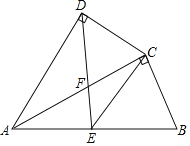
（2）如图2，过点P作PE⊥AC于E，

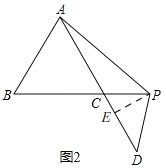
∴∠AEP＝90°，

∵△ABC是等边三角形，

∴AC＝2，∠ACB＝60°，

∴∠PCE＝60°，

在Rt△CPE中，CP＝1，∠CPE＝90°﹣∠PCE＝30°，

∴CE＝CP＝，

根据勾股定理得，PE＝，

在Rt△APE中，AE＝AC+CE＝2+＝，

根据勾股定理得，AP2＝AE2+PE2＝7，

∵∠ACB＝60°，

∴∠ACP＝120°＝∠APD，

∵∠CAP＝∠PAD，

∴△ACP∽△APD，

∴，

∴AD＝＝；

（3）如图3，由（2）知，AD＝，

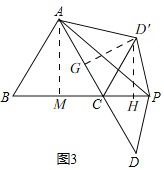
∵AC＝2，

∴CD＝AD﹣AC＝，

由旋转知，∠DCD'＝120°，CD'＝CD＝，

∵∠DCP＝60°，

∴∠ACD'＝∠DCP＝60°，

过点D'作D'H⊥CP于H，

在Rt△CHD'中，CH＝CD'＝，

根据勾股定理得，D'H＝CH＝，

过点D'作D'G⊥AC于G，

∵∠ACD'＝∠PCD'，

∴D'G＝D'H＝（角平分线定理），

∴S四边形ACPD'＝S△ACD'+S△PCD'＝ACD'G+CPDH'＝×2×+×1×＝，

过点A作AM⊥BC于M，

∵AB＝AC，

∴BM＝BC＝1，

在Rt△ABM中，根据勾股定理得，AM＝BM＝，

∴S△ACP＝CPAM＝×1×＝，

∴S△D'AP＝S四边形ACPD'﹣S△ACP＝﹣＝．