题目内容
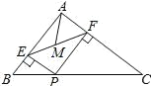
【题目】如图，
与
有公共边
，且
，
，
，
，
的角平分线
交
于点
，连接
.
（1）求
的度数；
（2）若
，
，求的长.
【答案】（1）
（2）
.
【解析】
（1）根据题意，易得△BCD和△ABC都为等腰三角形，所以延长CE与AB相交于F,根据三线合一可知CF⊥AB，F为AB的中点，根据垂直平分线的性质和等腰三角形等边对等角可得
，求出∠ABE的度数，根据三角形内角和定理即可求出
；
（2）根据含30°角的直角三角形的特点分别求得AF和EF，再证明△ACF为等腰三角形即可求出CF，由
可求.
解：（1）如下图，延长CE与AB相交于F，
∵AC=BC，
，
∴
,
∵
的角平分线
交
于点
，
∴CF⊥AB，F为AB的中点，
∴EA=EB，
∴，
∵
，
，
∴
，
∴
，
∴
.
（2）∵
，
，CF⊥AB，
∴
,
∵
，
∴
，
∴
,
∴
.
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
