题目内容
如图,直线y=k1x+b与反比例函数 的图象交于A(1,6),B(a,3)两点.
的图象交于A(1,6),B(a,3)两点.
(1)求k1、k2的值;
(2)结合图形,直接写出 时,x的取值范围;
时,x的取值范围;
(3)连接AO、BO,求△ABO的面积;
(4)如图2,梯形OBCE中,BC∥OE,过点C作CE⊥X轴于点E,CE和反比例函数的图象交于点P,当梯形OBCE的面积为9时,请判断PC和PE的大小关系,并说明理由.

解:(1)把A(1,6)代入y=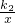 得,k2=1×6=6,
得,k2=1×6=6,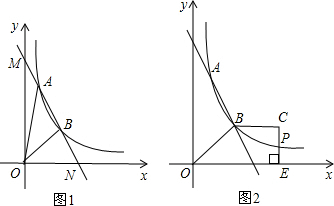
所有反比例函数的解析式为y= ,
,
把B(a,3)代入y= 得,3=
得,3= ,解得a=2,
,解得a=2,
所有B点坐标为(2,3),
把A(1,6)、B(2,3)代入y=k1x+b得,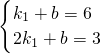 ,解得
,解得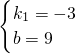 ,
,
所有k1、k2的值分别为-3,6;
(2)1<x<2时, ;
;
(3)直线y=-3x+9交坐标轴于M、N,如图1,
则M点坐标为(0,9),N点坐标为(3,0),
∴S△ABO=S△AON-S△BON= ×3×6-
×3×6- ×3×3=
×3×3= ;
;
(4)PC=PE.理由如下:
∵四边形OBDE为梯形,
∴BC∥OE,
而B点坐标为(2,3),
∴C点的纵坐标为3,
设C点坐标为(a,3),
∵CE⊥x轴,
∴E点坐标为(a,0),P点的横坐标为a,
∵P点在y= 的图象上,
的图象上,
∴P点坐标为(a, ),
),
∵梯形OBCE的面积为9,
∴ (BC+OE)×CE=9,即
(BC+OE)×CE=9,即 (a+a-2)×3=9,解得a=4,
(a+a-2)×3=9,解得a=4,
∴C点坐标为(4,3),P点坐标为(4, ),E点坐标为(4,0),
),E点坐标为(4,0),
∴PC=3- =
= ,PE=
,PE= -0=
-0= ,
,
∴PC=PE.
分析:(1)先把A(1,6)代入y=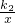 可求得k2=1×6=6,再把B(a,3)代入y=
可求得k2=1×6=6,再把B(a,3)代入y= 可得a=2,即B点坐标为(2,3),然后把A(1,6)、B(2,3)代入y=k1x+b得到关于k1、b的方程组,解方程组得到得
可得a=2,即B点坐标为(2,3),然后把A(1,6)、B(2,3)代入y=k1x+b得到关于k1、b的方程组,解方程组得到得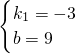 .
.
(2)观察图象得到当x<0或1<x<2时,直线y=k1x+b都在反比例函数 的图象上方,即
的图象上方,即 ;
;
(3)直线y=-3x+9交坐标轴于M、N,先求出M与N的坐标,然后利用S△ABO=S△AON-S△BON计算即可;
(4)根据梯形的性质得到BC∥OE,则由B点坐标为(2,3),得到C点的纵坐标为3,设C点坐标为(a,3),则E点坐标为(a,0),P点的横坐标为a,利用P点在y= 的图象上,则P点坐标为(a,
的图象上,则P点坐标为(a, ),根据梯形的面积公式得到
),根据梯形的面积公式得到 (BC+OE)×CE=9,即
(BC+OE)×CE=9,即 (a+a-2)×3=9,解得a=4,易得PC=3-
(a+a-2)×3=9,解得a=4,易得PC=3- ,PE=
,PE= -0=
-0= ,于是有PC=PE.
,于是有PC=PE.
点评:本题考查了反比例函数综合题:点在反比例函数图象上,点的横纵坐标满足反比例函数图象的解析式;平行于x轴的直线上的所有点的纵坐标相同;平行于y轴的直线上的所有点的横坐标相同;合理运用梯形的性质和面积公式建立等量关系.
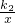 得,k2=1×6=6,
得,k2=1×6=6,
所有反比例函数的解析式为y=
 ,
,把B(a,3)代入y=
 得,3=
得,3= ,解得a=2,
,解得a=2,所有B点坐标为(2,3),
把A(1,6)、B(2,3)代入y=k1x+b得,
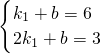 ,解得
,解得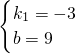 ,
,所有k1、k2的值分别为-3,6;
(2)1<x<2时,
 ;
;(3)直线y=-3x+9交坐标轴于M、N,如图1,
则M点坐标为(0,9),N点坐标为(3,0),
∴S△ABO=S△AON-S△BON=
 ×3×6-
×3×6- ×3×3=
×3×3= ;
;(4)PC=PE.理由如下:
∵四边形OBDE为梯形,
∴BC∥OE,
而B点坐标为(2,3),
∴C点的纵坐标为3,
设C点坐标为(a,3),
∵CE⊥x轴,
∴E点坐标为(a,0),P点的横坐标为a,
∵P点在y=
 的图象上,
的图象上,∴P点坐标为(a,
 ),
),∵梯形OBCE的面积为9,
∴
 (BC+OE)×CE=9,即
(BC+OE)×CE=9,即 (a+a-2)×3=9,解得a=4,
(a+a-2)×3=9,解得a=4,∴C点坐标为(4,3),P点坐标为(4,
 ),E点坐标为(4,0),
),E点坐标为(4,0),∴PC=3-
 =
= ,PE=
,PE= -0=
-0= ,
,∴PC=PE.
分析:(1)先把A(1,6)代入y=
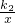 可求得k2=1×6=6,再把B(a,3)代入y=
可求得k2=1×6=6,再把B(a,3)代入y= 可得a=2,即B点坐标为(2,3),然后把A(1,6)、B(2,3)代入y=k1x+b得到关于k1、b的方程组,解方程组得到得
可得a=2,即B点坐标为(2,3),然后把A(1,6)、B(2,3)代入y=k1x+b得到关于k1、b的方程组,解方程组得到得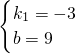 .
.(2)观察图象得到当x<0或1<x<2时,直线y=k1x+b都在反比例函数
 的图象上方,即
的图象上方,即 ;
;(3)直线y=-3x+9交坐标轴于M、N,先求出M与N的坐标,然后利用S△ABO=S△AON-S△BON计算即可;
(4)根据梯形的性质得到BC∥OE,则由B点坐标为(2,3),得到C点的纵坐标为3,设C点坐标为(a,3),则E点坐标为(a,0),P点的横坐标为a,利用P点在y=
 的图象上,则P点坐标为(a,
的图象上,则P点坐标为(a, ),根据梯形的面积公式得到
),根据梯形的面积公式得到 (BC+OE)×CE=9,即
(BC+OE)×CE=9,即 (a+a-2)×3=9,解得a=4,易得PC=3-
(a+a-2)×3=9,解得a=4,易得PC=3- ,PE=
,PE= -0=
-0= ,于是有PC=PE.
,于是有PC=PE.点评:本题考查了反比例函数综合题:点在反比例函数图象上,点的横纵坐标满足反比例函数图象的解析式;平行于x轴的直线上的所有点的纵坐标相同;平行于y轴的直线上的所有点的横坐标相同;合理运用梯形的性质和面积公式建立等量关系.

练习册系列答案
相关题目
 11、如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为
11、如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为 9、如图,直线y1=k1x+a与y2=k3x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( )
9、如图,直线y1=k1x+a与y2=k3x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( ) 如图,直线y=k1x与双曲线y=
如图,直线y=k1x与双曲线y= (2013•阜宁县一模)如图,直线y=k1x-b与双曲线
(2013•阜宁县一模)如图,直线y=k1x-b与双曲线 (2013•甘井子区一模)如图,直线y=k1x+b与双曲线
(2013•甘井子区一模)如图,直线y=k1x+b与双曲线