题目内容
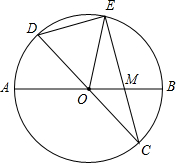
已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,DE= .
.
(1)求证: ;
;
(2)求EM的长;
(3)求sin∠EOB的值.
(1)证明:连接AC、EB
∵∠A=∠BEC,∠B=∠ACE
∴△AMC∽△EMB
∴
∴ --------------------------------------------------------3分
--------------------------------------------------------3分
(2)解:∵DC是⊙O的直径
∴∠DEC=90°
∴
∵DE= ,CD=8,且EC为正数
,CD=8,且EC为正数
∴EC=7
∵M为OB的中点
∴BM=2,AM=6
∵ ,且EM>MC
,且EM>MC
∴EM=4------------------------------------------------------------------------------7分
(3)解:过点E作EF⊥AB,垂足为点F
∵OE=4,EM=4
∴OE=EM
∴OF=FM=1
∴EF=
∴sin∠EOB= ---------------------------------------------------------------------10分
---------------------------------------------------------------------10分
解析

练习册系列答案
相关题目
 于点E,且EM>MC.连接DE,DE=
于点E,且EM>MC.连接DE,DE=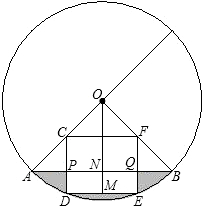 已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧
已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧
 上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.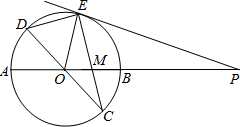 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=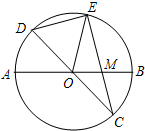 已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=