题目内容
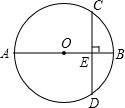
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OA=5,AB=8,求tan∠AEB的大小.
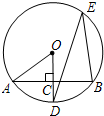
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OA=5,AB=8,求tan∠AEB的大小.

(1)∵OD⊥AB,
∴
=
,
∴∠DEB=
∠AOD=
×52°=26°.(4分)
(2)∵OD⊥AB,
∴弧AD=弧BD=
弧AB,
∴AC=BC=
AB=4,△AOC为直角三角形,
∴∠AEB=∠AOD,
∵OA=5,由勾股定理可得OC=
=3,
∴tan∠AEB=
=
.
∴
 |
| AD |
 |
| DB |
∴∠DEB=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵OD⊥AB,
∴弧AD=弧BD=
| 1 |
| 2 |
∴AC=BC=
| 1 |
| 2 |
∴∠AEB=∠AOD,
∵OA=5,由勾股定理可得OC=
| 52-42 |
∴tan∠AEB=
| AC |
| OC |
| 4 |
| 3 |

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目