题目内容
 如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC与AC的中点,P是AB上一点,以PF为一直角边作等腰直角△PFQ,且∠FPQ=90°,若AB=8,PB=1,则QE=
如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC与AC的中点,P是AB上一点,以PF为一直角边作等腰直角△PFQ,且∠FPQ=90°,若AB=8,PB=1,则QE=考点:相似三角形的判定与性质,等腰直角三角形
专题:
分析:取AB中点D,连接FD,根据等腰直角三角形的性质,由△ABC为等腰直角三角形得到AC=BC=4
,∠A=45°,再根据点D、E、F分别是△ABC三边的中点,则AD=BD=4,DP=3,EF为△ABC的中位线,于是可判断△ADF为等腰直角三角形,得到∠FDA=45°,利用三角形中位线的性质得EF∥AB,EF=
AB=4,根据平行线性质得∠EFP+∠DFP=45°;又由于△PQF为等腰直角三角形,则∠EFP+∠EFQ=45°,所以∠DFP=∠EFQ,然后根据有两组对应边成比例且夹角相等的三角形相似,得出△FDP∽△FEQ,再根据相似三角形的对应边成比例即可求得.
| 2 |
| 1 |
| 2 |
解答: 解:连结FD,D是AB的中点,如图,
解:连结FD,D是AB的中点,如图,
∵△ABC为等腰直角三角形,AB=8,PB=1,
∴AC=BC=4
,∠A=45°,
∵点D、E、F分别是△ABC三边的中点,AB=8,PB=1,
∴AD=BD=4,DP=DB-PB=4-1=3,EF、DF为△ABC的中位线,
∴EF∥AB,EF=
AB=4,DF=
BC=2
,∠EFP=∠FPD,
∴∠FDA=45°,
=
∴∠DFP+∠DPF=45°,
∵△PQF为等腰直角三角形,
∴∠PFE+∠EFQ=45°,FP=FQ,
∴∠DFP=∠EFQ,
∵△PFQ是等腰直角三角形,
∴
=
,
∴
=
,
∴△FDP∽△FEQ,
∴
=
=
,
∴QE=
•DP=3
故答案为:3
.
 解:连结FD,D是AB的中点,如图,
解:连结FD,D是AB的中点,如图,∵△ABC为等腰直角三角形,AB=8,PB=1,
∴AC=BC=4
| 2 |
∵点D、E、F分别是△ABC三边的中点,AB=8,PB=1,
∴AD=BD=4,DP=DB-PB=4-1=3,EF、DF为△ABC的中位线,
∴EF∥AB,EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴∠FDA=45°,
| DF |
| EF |
| ||
| 2 |
∴∠DFP+∠DPF=45°,
∵△PQF为等腰直角三角形,
∴∠PFE+∠EFQ=45°,FP=FQ,
∴∠DFP=∠EFQ,
∵△PFQ是等腰直角三角形,
∴
| PF |
| FQ |
| ||
| 2 |
∴
| DF |
| EF |
| PF |
| FQ |
∴△FDP∽△FEQ,
∴
| QE |
| DP |
| EF |
| FD |
| 2 |
∴QE=
| 2 |
| 2 |
故答案为:3
| 2 |
点评:本题考查了相似三角形的判定:两组对应边成比例且夹角相等的两个三角形相似,相似三角形的对应边成比例,也考查了等腰直角三角形的判定与性质.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 如图,已知⊙O是△ABC的外接圆,AB=AC,D是直线BC上一点,直线AD交⊙O于点E,AE=9,DE=3,则AB的长等于( )
如图,已知⊙O是△ABC的外接圆,AB=AC,D是直线BC上一点,直线AD交⊙O于点E,AE=9,DE=3,则AB的长等于( )| A、7 | ||
B、3
| ||
C、2
| ||
D、3
|
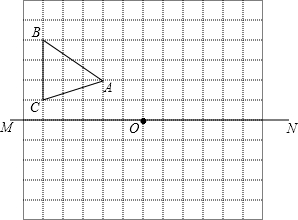 如图,在边长都是1个单位长度的正方形网格中,有一个△ABC.
如图,在边长都是1个单位长度的正方形网格中,有一个△ABC.