题目内容
设n为自然数,且an=
+
+
,则
+
+…+
+
= .
| 3 | n2+2n+1 |
| 3 | n2-1 |
| 3 | n2-2n+1 |
| 1 |
| a1 |
| 1 |
| a3 |
| 1 |
| a997 |
| 1 |
| a999 |
考点:有理数无理数的概念与运算
专题:
分析:运用乘法公式(a-b)(a2+ab+b2)=a3-b3,求出an的倒数,得出一般规律,再计算算式.
解答:解:由已知得an=(n+1)
+(n+1)
•(n-1)
+(n-1)
,
而[(n+1)
-(n-1)
][(n+1)
+(n+1)
•(n-1)
+(n-1)
]
=[(n+1)
]3-[(n-1)
]3
=(n+1)-(n-1)
=2,
即[(n+1)
-(n-1)
]•an=2,
所以
=
(
-
),
则
+
+…+
+
=
(
-0+
-
+
-
+…+
-
+
-
)
=
×
=
×10
=5.
故答案为:5.
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
而[(n+1)
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
=[(n+1)
| 1 |
| 3 |
| 1 |
| 3 |
=(n+1)-(n-1)
=2,
即[(n+1)
| 1 |
| 3 |
| 1 |
| 3 |
所以
| 1 |
| an |
| 1 |
| 2 |
| 3 | n+1 |
| 3 | n-1 |
则
| 1 |
| a1 |
| 1 |
| a3 |
| 1 |
| a997 |
| 1 |
| a999 |
=
| 1 |
| 2 |
| 3 | 2 |
| 3 | 4 |
| 3 | 2 |
| 3 | 6 |
| 3 | 4 |
| 3 | 998 |
| 3 | 996 |
| 3 | 1000 |
| 3 | 998 |
=
| 1 |
| 2 |
| 3 | 1000 |
=
| 1 |
| 2 |
=5.
故答案为:5.
点评:本题考查了有理数无理数的概念与运算.关键是分析an的式子结构特点,利用乘法公式推出一般规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
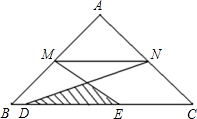 如图所示,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM,若AB=10cm,BC=16cm,DE=8cm,则图中阴影部分的面积为( )
如图所示,在△ABC中,AB=AC,M、N分别是AB、AC的中点,D、E为BC上的点,连接DN、EM,若AB=10cm,BC=16cm,DE=8cm,则图中阴影部分的面积为( )| A、4cm2 |
| B、6cm2 |
| C、8cm2 |
| D、12cm2 |

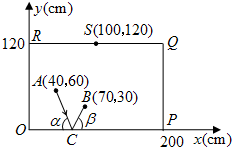 实验探究:下面设想用电脑模拟台球游戏,为简单起见,约定:①每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;②A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;③球撞及桌边后的反弹角等于入射角.
实验探究:下面设想用电脑模拟台球游戏,为简单起见,约定:①每个球或球袋都视为一点,如不遇障碍,各球均沿直线前进;②A球击中B球,意味着B球在A球前进的路线上,且B球被撞击后沿着A球原来的方向前进;③球撞及桌边后的反弹角等于入射角.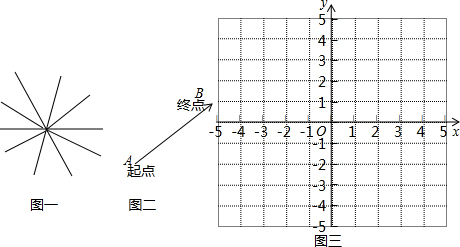
 如图所示,堆放的一堆钢管共110根,最上面的一层有5根,每往下一层就增加一根,如果每根钢管的直径为10厘米,那么这堆钢管的总高度是
如图所示,堆放的一堆钢管共110根,最上面的一层有5根,每往下一层就增加一根,如果每根钢管的直径为10厘米,那么这堆钢管的总高度是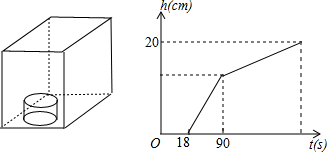 .水槽中水面上升的高度h与注水时间t之间的函数关系如图所示.
.水槽中水面上升的高度h与注水时间t之间的函数关系如图所示.