题目内容
已知：抛物线的顶点为（-1，3），且经过点（1，-1），求这条抛物线的函数关系式．
解：已知抛物线的顶点为（-1，3），可设y=a（x+1）2+3，
将点（1，-1）代入y=a（x+1）2+3中，得：
4a+3=-1，解得a=-1，
∴这条抛物线的函数关系式y=-（x+1）2+3．
分析：根据题意可设顶点式y=a（x+1）2+3，将点（1，-1）代入可求a，从而确定抛物线解析式．
点评：本题考查了用待定系数法求函数解析式的方法，当二次函数的顶点坐标已知时，可设顶点式．
将点（1，-1）代入y=a（x+1）2+3中，得：
4a+3=-1，解得a=-1，
∴这条抛物线的函数关系式y=-（x+1）2+3．
分析：根据题意可设顶点式y=a（x+1）2+3，将点（1，-1）代入可求a，从而确定抛物线解析式．
点评：本题考查了用待定系数法求函数解析式的方法，当二次函数的顶点坐标已知时，可设顶点式．
练习册系列答案
相关题目
已知：抛物线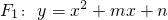
的顶点为A（1，0）
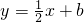交x轴于点C，交y轴于点D，在抛物线F1上有一点B，且点B与点A关于直线
？若存在试求n的值；若不存在，请说明理由．
的顶点为A，与x轴的交点为B，C（点B
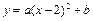
的顶点为A，与x轴的交点为B，C（点B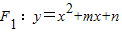
的顶点为A（1，0）
交x轴于点C，交y轴于点D，在抛物线F1上有一点B，且点B与点A关于直线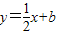
对称，若抛物线F2的顶点为点B，且经过点A，试求抛物线F2的函数解析式；
？若存在试求n的值；若不存在，请说明理由．