题目内容
已知:抛物线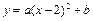
 的顶点为A,与x轴的交点为B,C(点B
的顶点为A,与x轴的交点为B,C(点B
在点C的左侧).
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC为直角三角形,求a,b的值;
(3)若D为抛物线对称轴上一点,则以A,B,C,D为顶点的四边形能否为正方形?若能,请写出a,b满足的关系式;若不能,说明理由.

解:(1)抛物线对称轴方程: . ………2分
. ………2分
(2)设直线 与
与 轴交于点E,则E(2,0).
轴交于点E,则E(2,0).
∵抛物线经过原点, ∴B(0,0),C(4,0). ………3分
∵△ABC为直角三角形,根据抛物线的对称性可知 ,
,
∴ ,
,
∴A(2,-2)或(2,2).
当抛物线的顶点为A(2,-2)时, ,把(0,0)代入,得:
,把(0,0)代入,得: ,此时,
,此时, . ………5分
. ………5分
当抛物线的顶点为A(2,2)时, ,把(0,0)代入,得:
,把(0,0)代入,得: ,此时,
,此时, .
.
∴ ,
, 或
或 ,
, . ………7分
. ………7分
(3)依题意,B、C关于点E中心对称,当A,D也关于点E对称,且 时,四边形ABDC是正方形.
时,四边形ABDC是正方形.
∵ , ∴
, ∴ , ∴
, ∴ ,
,
把 代入
代入 ,得
,得  ,
,
∵ , ∴
, ∴ . ………10分
. ………10分
解析

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 已知:抛物线的顶点坐标为C(1,4),抛物线交x轴于点A,交y轴于点B(0,3).
已知:抛物线的顶点坐标为C(1,4),抛物线交x轴于点A,交y轴于点B(0,3). (2013•青羊区一模)如图,抛物线y=ax2+bx+c与x轴有两个不同的交点A(x1,0)、B(x2,0)(x1<x2),与y轴的正半轴交于点C(0,3).已知该抛物线的顶点横坐标为1,A、B两点间的距离为4.
(2013•青羊区一模)如图,抛物线y=ax2+bx+c与x轴有两个不同的交点A(x1,0)、B(x2,0)(x1<x2),与y轴的正半轴交于点C(0,3).已知该抛物线的顶点横坐标为1,A、B两点间的距离为4. 已知:抛物线
已知:抛物线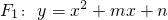 的顶点为A(1,0)
的顶点为A(1,0)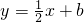 交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线
交x轴于点C,交y轴于点D,在抛物线F1上有一点B,且点B与点A关于直线 ?若存在试求n的值;若不存在,请说明理由.
?若存在试求n的值;若不存在,请说明理由.
 的顶点为A,与x轴的交点为B,C(点B
的顶点为A,与x轴的交点为B,C(点B