题目内容
9.若两条抛物线的顶点相同,则称它们为“友好抛物线”,已知抛物线C1:y1=-x2+ax+b与抛物线C2:y2=2x2+4x+6为“友好抛物线”,抛物线C1与x轴交于点A、C,与y轴交于点B.(1)求抛物线C1的表达式.
(2)若F(t,0)(-3<t<0)是x轴上的一点,过点F作x轴的垂线交抛物线与点P,交直线AB于点E,过点P作PD⊥AB于点D.
①是否存在点F,使PE+PD的值最大,若存在,请求出t的值;若不存在,请说明理由.
②连接PA,以AP为边作图示一侧的正方形APMN,随着点F的运动,正方形的大小、位置也随之改变.当正方形APMN中的边MN与y轴有且仅有一个交点时,求t的取值范围.
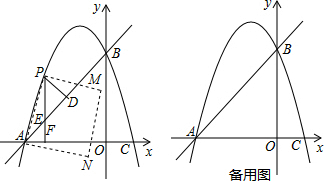
分析 (1)求出抛物线C1的顶点坐标即可解决问题;
(2)①首先证明△PDE是等腰直角三角形,可知PD越大,PE+PD的值越大,易得直线AB的解析式为y=x+3,设与AB平行的直线解析式为y=x+m,联立 $\left\{\begin{array}{l}{y=x+m}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,消掉y得,x2+3x+m-3=0,当△=32-4×1×(m-3)=0,即m=$\frac{21}{4}$时,直线与抛物线只有一个交点,PD最长,由此即可解决问题;
②分两种情形(i)如图1中,当点M在y轴上时,(ii)如图2,点N在y轴上时,分别求解即可;
解答 解:(1)由y2=2x2+4x+6=2(x+1)2+4,可知顶点坐标为(-1,4),
∵知抛物线C1:y1=-x2+ax+b与抛物线C2:y2=2x2+4x+6为“友好抛物线”,
∴顶点相同,抛物线C1的解析式为y1=-(x+1)2+4,
即y1=-x2-2x+3.
(2)①由题意易知A(-3,0),B(0,3),
∴OA=OB=3,
∴△AOB是等腰直角三角形,
∴∠BAO=45°,
∵PF⊥x轴,
∴∠AEF=90°-45°=45°,
又∵PD⊥AB,
∴△PDE是等腰直角三角形,
∴PD越大,PE+PD的值越大,
易得直线AB的解析式为y=x+3,
设与AB平行的直线解析式为y=x+m,
联立 $\left\{\begin{array}{l}{y=x+m}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,
消掉y得,x2+3x+m-3=0,
当△=32-4×1×(m-3)=0,
即m=$\frac{21}{4}$时,直线与抛物线只有一个交点,PD最长,
此时x=-$\frac{3}{2}$,y=-$\frac{3}{2}$+$\frac{21}{4}$=$\frac{15}{4}$,
∴点P(-$\frac{3}{2}$,$\frac{15}{4}$)时,PD+PE的值最大,
此时t=-$\frac{3}{2}$.
②抛物线y=-x2-2x+3的对称轴为直线x=-$\frac{-2}{2×(-1)}$=-1,
(i)如图1,当点M在y轴上时,过点P作PQ⊥y轴于Q,
在正方形APMN中,AP=PM,∠APM=90°,
∴∠APF+∠FPM=90°,∠QPM+∠FPM=90°,
∴∠APF=∠QPM,
∵在△APF和△MPQ中,
$\left\{\begin{array}{l}{∠APF=∠QPM}\\{∠AFP=∠MQP}\\{AP=PM}\end{array}\right.$,
∴△APF≌△MPQ(AAS),
∴PF=PQ,
∵点P的横坐标为t(t<0),则PQ=-t,
即PF=-t,
∴点P的坐标为(t,-t),
∵点P在抛物线y=-x2-2x+3上,
∴-t2-2t+3=-t,
整理得,t2+t-3=0,
解得t1=$\frac{-1+\sqrt{13}}{2}$(舍去),t2=$\frac{-1-\sqrt{13}}{2}$,
(ii)如图2,点N在y轴上时,
∵∠PAF+∠FPA=90°,∠PAF+∠QAN=90°,
∴∠FPA=∠QAN,
又∵∠PFA=∠AQN=90°,PA=AN,
∴△APF≌△NAO,
∴PF=AO,
则点P坐标为P(t,3),
则有-t2-2t+3=3,解得x=-2或0,
观察图象可知,当正方形APMN中的边MN与y轴有且仅有一个交点时,t的取值范围为$\frac{-1-\sqrt{13}}{2}$≤t≤-2.
点评 本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,等腰直角三角形的判定与性质,正方形的性质,全等三角形的判定与性质,抛物线上点的坐标特征,(2)确定出△PDE是等腰直角三角形,从而判断出点P为平行于AB的直线与抛物线只有一个交点时的位置是解题的关键,(3)根据全等三角形的性质用点P的横坐标表示出纵坐标或用纵坐标求出横坐标是解题的关键.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | 事件A和B都是随机事件 | |
| B. | 事件A是随机事件,事件B是不可能事件 | |
| C. | 事件A是必然事件,事件B是随机事件 | |
| D. | 事件A和事件B都是必然事件 |
| A. | y=-2x+1 | B. | y=1+2x | C. | -y=2x+1 | D. | y-1=2x |
| 分数 | 87 | 88 | 90 | 93 | 97 |
| 人数 | 2 | 3 | 4 | 2 | 1 |
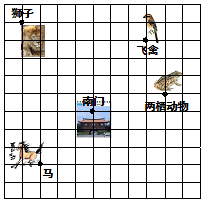 这是一个动物园游览示意图,如果以南门为坐标原点,东西为x轴,南北为y轴,
这是一个动物园游览示意图,如果以南门为坐标原点,东西为x轴,南北为y轴,