题目内容
19.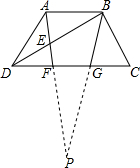 在梯形ABCD中,AB∥CD,点F,G是下底CD的三等分点,BG与AF的延长线交于点P,AF与BD交于点E,求证:PF•AE=PA•EF.
在梯形ABCD中,AB∥CD,点F,G是下底CD的三等分点,BG与AF的延长线交于点P,AF与BD交于点E,求证:PF•AE=PA•EF.
分析 由AB∥CD,得到△ABE∽△DEF,△ABP∽△FGP,求得$\frac{AE}{EF}=\frac{AB}{DF}$,$\frac{AB}{FG}=\frac{PA}{PF}$,等量代换得到$\frac{AE}{EF}=\frac{PA}{PF}$,于是得到结论.
解答 解:∵AB∥CD,
∴△ABE∽△DEF,△ABP∽△FGP,
∴$\frac{AE}{EF}=\frac{AB}{DF}$,$\frac{AB}{FG}=\frac{PA}{PF}$,
∵点F,G是下底CD的三等分点,
∴DF=FG,
∴$\frac{AE}{EF}=\frac{PA}{PF}$,
∴PF•AE=PA•EF.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
11.用科学记数法表示的数为2.25×105,则原数是( )
| A. | 22500 | B. | 225000 | C. | 2250000 | D. | 2250 |
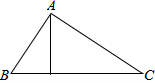 如图,点A表示一个半径为400米的森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=37°,如果在两村庄之间修一条长1000m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?请说明理由.(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
如图,点A表示一个半径为400米的森林公园的中心,在森林公园附近有B、C两个村庄,且∠B=45°,∠C=37°,如果在两村庄之间修一条长1000m的笔直公路将两村连通,那么该公路是否会穿过该森林公园?请说明理由.(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)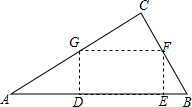 如图,在直角△ABC中,∠C=90°,AC=8,BC=6,在△ABC中裁剪出矩形DEFG.则下列结论一定成立的是①②(把所有正确结论的序号都填在横线上).
如图,在直角△ABC中,∠C=90°,AC=8,BC=6,在△ABC中裁剪出矩形DEFG.则下列结论一定成立的是①②(把所有正确结论的序号都填在横线上).