题目内容
4．
如图，正方形ABCD内接于⊙O，异于D、C的动点P在$\widehat{CD}$上，则∠BPC=45°．
分析 连接OB、OC，根据正方形的性质得到∠BOC=90°，根据圆周角定理解答即可．
解答 解：
连接OB、OC，
∵四边形ABCD是正方形，
∴∠BOC=90°，
由圆周角定理得，∠BPC=$\frac{1}{2}$∠BOC=45°，
故答案为：45°．
点评 本题考查的是正方形的性质和圆周角定理，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解题的关键．
练习册系列答案
相关题目
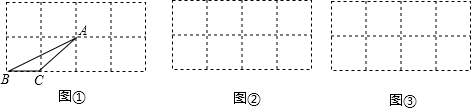
15．
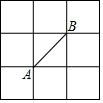如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（ ）
如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数是（ ）| A． | 6 个 | B． | 7 个 | C． | 8 个 | D． | 9个 |
如图，一块正方形的铁皮，边长为x cm（x＞4），如果一边截去宽4cm的一块，相邻一边截去宽3cm的一块．