Question

6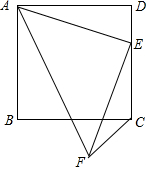．正方形ABCD中，E为DC边上一点，且DE=1，将AE绕点E顺时针旋转90°得到EF，连接AF，FC，则FC=$\sqrt{2}$．

Answer 1

分析 作FH⊥CD于H，如图，利用正方形的性质得DA=CD，∠D=90°，再根据旋转的性质得EA=EF，∠AEF=90°，接着证明△ADE≌△EHF得到DE=FH=1，AD=EH，所以EH=DC，则DE=CH=1，然后利用勾股定理计算FC的长．

解答 解：作FH⊥CD于H，如图，
∵四边形ABCD为正方形，
∴DA=CD，∠D=90°，
∵AE绕点E顺时针旋转90°得到EF，
∴EA=EF，∠AEF=90°，
∵∠DAE+∠AED=90°，∠FEH+∠AED=90°，
∴∠EAD=∠FEH，
在△ADE和△EHF中
$\left\{\begin{array}{l}{∠D=∠FHE}\\{∠EAD=∠FEH}\\{AE=EF}\end{array}\right.$，
∴△ADE≌△EHF，
∴DE=FH=1，AD=EH，
∴EH=DC，
即DE+CE=CH+EC，
∴DE=CH=1，
在Rt△CFH中，FC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$．
故答案为$\sqrt{2}$．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．