题目内容
求下列各式中的x的值:
①|5x2-4|=6;
②|3x-4|+2|2x+1|=4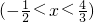 ;
;
③(x- )2=2;
)2=2;
④2(3x- )2=8.
)2=8.
解:①∵|5x2-4|=6,
∴5x2-4=6或5x2-4=-6,
∴x2=2或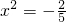 (舍去),
(舍去),
当x2=2时,x是2的平方根,
∴x=± ;
;
②∵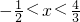 ,
,
∴2x>-1,3x<4,
∴2x+1>0,3x-4<0,
∴|3x-4|+2|2x+1|=-(3x-4)+2(2x+1)=x+6=4,
∴x=-2,
这与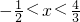 矛盾,故所求x不存在;
矛盾,故所求x不存在;
③∵(x- )2=2,
)2=2,
∴x- =±2,
=±2,
∴x=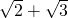 ;
;
④∵2(3x- )2=8,
)2=8,
∴(3x- )2=4,
)2=4,
∴3x- =±2,
=±2,
∴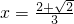 .
.
分析:①、③、④利用平方根的有关知识来解;
②根据x的取值范围,确定绝对值里面数的取值,再去绝对值符号.
点评:此题主要考查了求平方根的运算和绝对值的化简,其中分别利用了
(1)若x2=a,则x=± .
.
(2)|a|= .
.
∴5x2-4=6或5x2-4=-6,
∴x2=2或
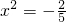 (舍去),
(舍去),当x2=2时,x是2的平方根,
∴x=±
 ;
;②∵
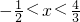 ,
,∴2x>-1,3x<4,
∴2x+1>0,3x-4<0,
∴|3x-4|+2|2x+1|=-(3x-4)+2(2x+1)=x+6=4,
∴x=-2,
这与
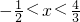 矛盾,故所求x不存在;
矛盾,故所求x不存在;③∵(x-
 )2=2,
)2=2,∴x-
 =±2,
=±2,∴x=
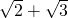 ;
;④∵2(3x-
 )2=8,
)2=8,∴(3x-
 )2=4,
)2=4,∴3x-
 =±2,
=±2,∴
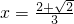 .
.分析:①、③、④利用平方根的有关知识来解;
②根据x的取值范围,确定绝对值里面数的取值,再去绝对值符号.
点评:此题主要考查了求平方根的运算和绝对值的化简,其中分别利用了
(1)若x2=a,则x=±
 .
.(2)|a|=
 .
. 
练习册系列答案
相关题目