��Ŀ����
��ͼ���ı���ABCD�������Σ���E��ֱ��BC�ϣ�����AE������ABE��AE����ֱ���۵�����B�Ķ�Ӧ���ǵ�B�䣬����AB�䲢�ӳ���ֱ��DC�ڵ�F��
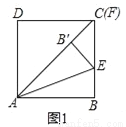
��1������F���C�غ�ʱ��ͼ1��֤����DF+BE=AF��
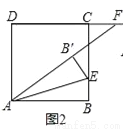
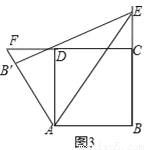
��2������F��DC���ӳ�����ʱ��ͼ2������F��CD���ӳ�����ʱ��ͼ3���߶�DF��BE��AF��������������ϵ����ֱ��д����IJ��룬��ѡ��һ���������֤����
��ϰ��ϵ�д�
 �߽�������ϵ�д�
�߽�������ϵ�д�
�����Ŀ


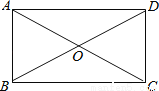
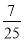 ����sinA��ֵΪ����
����sinA��ֵΪ����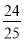 B.
B. 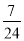 C.
C. 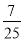 D.
D. 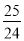
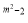 ��2x+10=0�ǹ���x��һԪ���η��̣���m��ֵΪ����
��2x+10=0�ǹ���x��һԪ���η��̣���m��ֵΪ����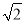 D. ��2
D. ��2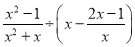 ������x=��2��
������x=��2��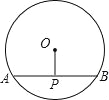
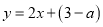 ��
��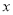 ��Ľ�����
��Ľ�����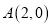 ��
�� 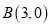 ֮�䣨����
֮�䣨����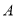 ��
�� 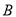 ���㣩��
���㣩��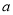 ��ȡֵ��Χ��__________��
��ȡֵ��Χ��__________��