题目内容
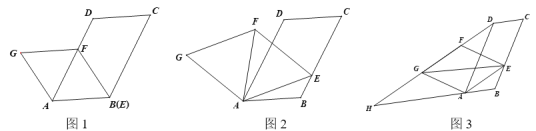
【题目】将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当∠B＝90°时，如图1，测得AC＝2，当∠B＝60°时，如图2，则BD=_________
【答案】
【解析】
连接BD，如图1中根据勾股定理即可求得正方形的边长，如图2中过点A作AE⊥BD，利用菱形的性质以及勾股定理即可BE的长，进而可求出BD的长．
解：如图甲，
∵AB=BC=CD=DA，∠B=90°，
∴四边形ABCD是正方形，
连接AC，则AB2+BC2=AC2=4，
∴AB=AD=
，
如图2，∠ABC=60°，连接BD，过点A作AE⊥BD于点E，
∴△ABD为等腰三角形，
∵AB=AD=，四边形ABCD是菱形，
∴∠ABE=30°，
∴AE=
AB=
，
∴BE=
，
∴BD=2BE=.
故答案为：.
练习册系列答案
相关题目
【题目】 黄石知名特产“黄石港饼”“白鸭牌松花皮蛋”“珍珠果米酒”一直以来享有美誉，深受人们喜爱．端午节快到了，为了满足市场需求，某公司组织20辆汽车装运港饼、皮蛋、米酒共120吨去外地销售，按计划20辆汽车都要装满，且每辆汽车只能装运同一类食品，根据下表提供的信息解答以下问题．
港饼 | 皮蛋 | 米酒 | |
每辆汽车载重量（吨） | 8 | 6 | 5 |
每吨食品获利（万元） | 0.2 | 0.4 | 0.6 |
（1）设装运港饼的车辆为x辆，装运皮蛋的车辆为y辆，求y与x之间的函数关系式；
（2）此次销售获利为W万元，试求W关于x的函数关系式；
（3）如果装运每种食品的车辆都不少于2辆，那么怎样安排车辆能使此次销售获利最大？并求出最大利润．
